Impulse

Impulse is the magnitude we use in dynamics to relate the force applied on a body to the time the force has been applied. It let us understand, for example, the mechanism of takeoff of the space shuttles, but also why football players put the ball behind their heads for the throw-in. In this chapter we are going to study it through the following points:

• Concept
• Definition
  • Impulse - momentum theorem
  • Variable force
• Graphs

Gather momentum!, let´s get started!

Concept

Have you ever ask yourself, why football players put the ball behind their heads to throw-in? That gesture does not increase considerably the value of the force to throw the ball but, however, it will let the players to exert the same force during more time. Players do what we know as gather momentum.

So, it seems clear that if we want to give a specific velocity to a body we have two options: to apply a bigger force during a shorter interval of time or, a smaller force during a longer interval of time. The longer the force applied is, the higher the speed we can get is.

impulse is the magnitude that let us quantify those ideas. Let´s define it formally.

Definition

Observe that, from the previous definition we can deduce that the impulse vector of a force possess the same direction than the force to which it´s associated. 

Impulse-momentum theorem

Taking into account that the variation of linear momentum can be related to the resultant force acting on a body according to:

$$\overrightarrow{F}=\frac{∆\overrightarrow{p}}{∆t}\Rightarrow \overrightarrow{F}·∆t = ∆\overrightarrow{p}$$

The product is the own definition we have given for the impulse, so that is related to the variation of the linear momentum of the body. It is the impulse-momentum theorem.

Observe that the previous expression brings to light the statement we did about that by giving a determined velocity to a body (to increase its linear momentum) we can act in two ways: by acting over the force or acting over the time on which it acts. So, in the space shuttles the ship get the desired speed due to the continuous effect of the force the motor drive provides.

It is normal to get confused. Bear in mind that their ecuations and dimensions are the same...

$$\left[J\right]=M·L·T^{-1}$$

... and the units of measure in the S.I. are equivalent...

$$N·s\equiv m·s^{-1}$$

Variable force

In the definition we have made of the linear impulse we assumed the force remains constant during the time interval ∆t acting. This is not like that in general, the force is variable though. We can, then, find the impulse acting  on the time interval infinitly small (diferential). That impulse would be a diferential impulse, and the force it would act on that time interval it would be constant, indeed. So:

$$\boxed{d\overrightarrow{J}=\overrightarrow{F}·dt}$$

So the impulse transferred during a finite time interval is obtained adding the finite diferential impulses by integrating:

$${\int }_{t_i}^{t_f}d\overrightarrow{J}={\int }_{t_i}^{t_f}\overrightarrow{F}·dt\Rightarrow \boxed{\overrightarrow{J}={\int }_{t_i}^{t_f}\overrightarrow{F}·dt}$$

Regarding the impulse theorem, we can get to the same statement already introduced for constant forces, considering this time as variable forces. In order to check it we must consider the differential version of the Newton´s second Law, that is $\overrightarrow{F}=\frac{d\overrightarrow{p}}{dt}$. So:

 

$$J={\int }_{t_i}^{t_f}\overrightarrow{F}·dt={\int }_{t_i}^{t_f}\frac{d\overrightarrow{p}}{\cancel{dt}}·\cancel{dt}={\int }_{t_i}^{t_f}d\overrightarrow{p}={\left[\overrightarrow{p}\right]}_{t_i}^{t_f}={\overrightarrow{p}}_f-{\overrightarrow{p}}_i=∆\overrightarrow{p}$$

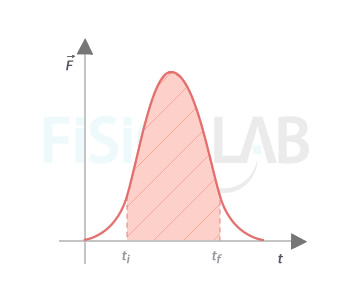
Impulse Charts

Probably you know now that the defined integral between two values of a function coincides numerically in value with the area set under that function. So, if we represent in the horizontal axis the time, and, the force in the vertical axis, either constant or variable, the area of the curve between  t_i and t_f coincides with the value of the impulse: 

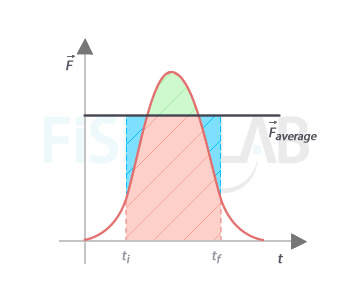
From this idea, watch that it is always possible to find an average constant force whose value of impulse in that time interval coincides with the one of the variable force.

Thus, most of the times on this level, when we talk about impulse force we are referring to that same assumed average constant force.