Ayúdanos a mantenernos en órbita
¿Nuestros contenidos te están resultando de utilidad?
Con un pequeño gesto podremos mantenernos en órbita. Regístrate para acceder a contenidos y funcionalidad exclusiva. Además, con tu ayuda podremos continuar ofreciendo nuestros servicios de manera gratuita para miles de estudiantes en todo el mundo. Te ofrecemos:
- Un campus virtual orientado a la gamificación
- Nuevos contenidos premium
- Nuevas simulaciones
- Acceso prioritario a nuestro plantel de profesores de física y matemáticas
Reference Frame
We want to propose a thought experiment: Imagine you are traveling in a bus. Siting in your seat, you can affirm, without fear to be mistaken, that the bus driver does not move while he is driving. After all, he does not change his position in relation to you. However, an observer siting on a park bench, who sees the bus pass by on the road would say that the driver was moving. The outside observer would see the driver in motion because the driver is changing his position in relation to the observer.
We can define a reference frame, also known as frame of reference or reference system, as a coordinate system in relation to which we are studying the motion of a body. It assumes the observer's position in relation to the observed phenomenon.
So far, two key concepts have emerged to understand the movement of a body.
- Its position
- The reference system
The reference system is very important in physics when we are going to study motion: It is fundamental to establish the position of the body being studied. Normally, in physics we use the system formed by the Cartesian axes and Cartesian coordinates as a reference frame. Such system is formed by 3 perpendicular axes (OX, OY, and OZ) called 3-dimensional space, although it is also possible to use just 2 axes (OX, OY) called 2 dimensional space or plane, and even a single axis (OX) known as 1 dimensional space or straight line.
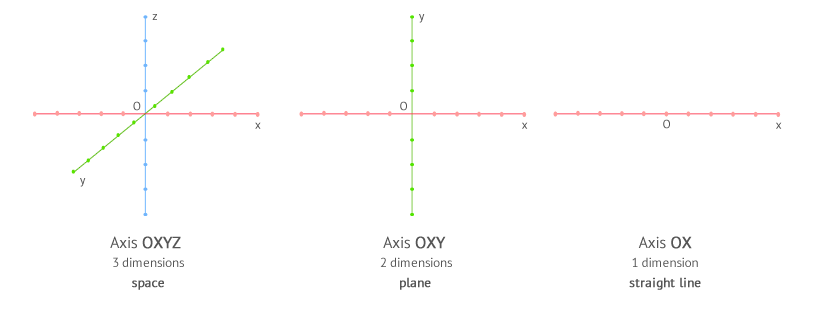
Remember, if you are studying the motion of a body that is occurring in one or two dimensions you can simplify your work by adequately choosing the reference system: in two dimensions, we only use two axes (generally OX and OY) and in one dimension we use one axis (generally OX).
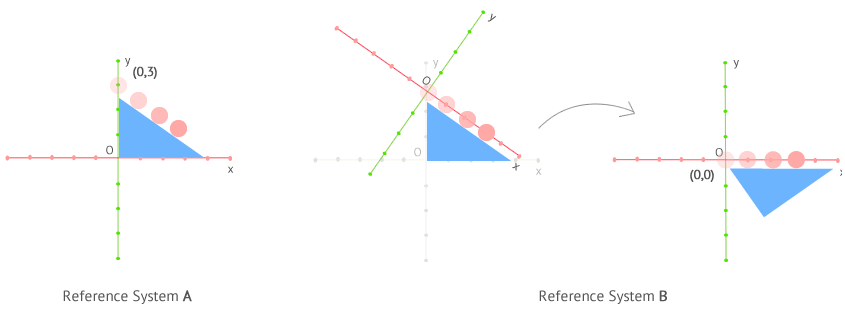
Occasionally, it is possible that the origin and orientation of the axes make it difficult to understand or to solve a problem, but we can always carry out transformations so that our system is adjusted to a more comfortable point of view. In the previous example, in which a ball is seen falling on an inclined plane, we could use a system as the one in A or as the one in B, whichever is more convenient for us. In A, the ball is moving in two dimensions (it changes its coordinates in the x and y axes as it moves) and in B, it moves in only one dimension (it only moves in the x axis). Making calculations in one dimension is generally easier than in two dimensions. So, it would be more convenient to choose system B.
In either case, we must make sure that the new references correspond to the change we have made in the system. For example, in A the ball starts to move at the point (0,3) and in B it start to move at (0,0).
Inertial and Non-inertial Reference Frames
Depending on their state of rest or relative movement, we can classify a reference frame in:
- Inertial Reference Frame. Said in simple terms, a reference frame is called inertial when it is fixed or its relative motion is uniform.
- Non-inertial Reference Frame. Simply, a non-inertial reference frame is one that is subjected to an acceleration.