It is important to note the difference between distance traveled and displacement since, in general, they are different concepts that are often confused. Distance traveled is a scalar magnitude that is measured over the trajectory. Displacement is a vector magnitude that depends only on the initial and final position of the body and which is independent of the trajectory. Imagine a body that moves on a circular path, thus returning to the starting point. The distance traveled by the body will be
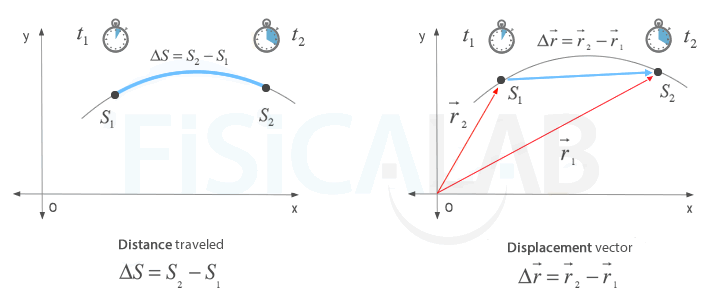
The following are some similarities and differences which can be deduced easily from the above.
| Displacement Vector | Distance traveled |
| Vector magnitude | Scalar magnitude |
| Depends on the initial and final points | It depends on the trajectory |
| Its magnitude coincides with the distance traveled when the trajectory is a straight line and there is no change of direction. | Its value matches the magnitude of the displacement vector when the trajectory is a straight line and there is no change of direction. |
| Its magnitude increases or decreases with the motion according to the trajectory described | Its magnitude always increases when the body is in motion, regardless of the trajectory |
| It is measured in meters | It is measured in meters |

