Average Velocity

The everyday concept of velocity arises when we consider how quick or slow a body is moving. Somehow we relate the displacement of the body with the time invested in it. In this section, we will define what is meant in physics by average velocity. This concept will help us understand other definitions related to velocity, that we will see in subsequent sections

Average velocity

The average velocity of a body that moves between two points P₁ and P₂ is defined as the ratio between the displacement vector and the time interval in which the displacement takes place. Its expression is given by:

{\vec{v}}_{a v g} = \frac{∆ \vec{r}}{∆ t} = \frac{\vec{r_{2}} - \vec{r_{1}}}{t_{2} - t_{1}}

where:

${\vec{v}}_{a v g}$ : Average velocity vector in the time studied
$∆ \vec{r}$ : Displacement vector in the time studied
$∆ t$ : Time taken by the body to complete the displacement
$\vec{r_{1}}$ , $\vec{r_{2}}$ : Position vectors of the corresponding initial P₁ and final P₂ positions
t₁, t₂ : Time in which the body is in the initial P₁ and final P₂ points respectively

Additionally, the average velocity vector meets the following:

If we use units of the International System (S.I.) in both the numerator (meters) and the denominator (seconds), we can deduce the dimensional equation of the average velocity [v]=[L][T]^-1
The unit of measurement in the International System (S.I.) for velocity is meter per second (m/s)
The magnitude (the "size" of the vector) is equal to the magnitude of the displacement vector divided by the elapsed time
The direction is the same as the direction of the displacement vector

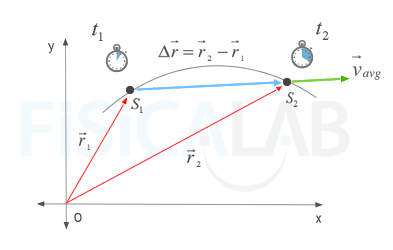
Average velocity

The average velocity of a body (green) is a vector that has the same direction as the displacement vector (blue) and its magnitude is the ratio between the magnitude of the displacement vector and the elapsed time.

It is important to notice that the average velocity of a body in a time interval depends of the position vectors at the beginning and at the end of the motion. Although it may seem paradoxical, this implies that if the initial and final position coincide in that interval, the average velocity of the body will be 0.

Experiment and Learn

Data

Average velocity vector

The graph shows the trajectory followed by a body over the time considered.

With the mouse, drag the initial position (at time t₁=0) and the final position (at time t₂) of the body anywhere you want. Then click and drag the circle indicating the time that the object will take to arrive at t₂ and press the Play button.

Notice how the body moves from the initial to the final position and the displacement vector (blue) is obtained, the position vector at each point (red) and the average velocity vector (green).

Observe that if we leave the points in the same place and reduce the time, the body will move faster and therefore the magnitude of the average velocity vector will be larger, if you increase the time then its magnitude will be smaller. Also, notice that the velocity vector has the same direction as the displacement vector.

Example

If a body is in the position (1,2) and after 2 seconds it is in the position (1,-2).

What will be its average velocity considering that all units are expressed in the International System?

Solution