Horizontal Launch

Horizontal launch is an example of composition of motion in two dimensions: an u.r.m. on the horizontal axis and a u.a.r.m. in the vertical one. In this section, we will see:

The concept and the representation of the horizontal launch
Its formulas
The equations of position in the horizontal launch

Are you ready?

Concept and representation

Horizontal launch consists of horizontally launching a body , also know as projectile, from a certain height. In the figure below you can see a representation of the situation:

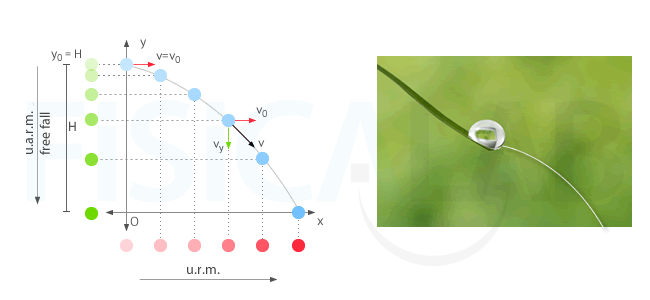
Horizontal launch

Think about a drop that slides at constant velocity (v₀) on a leaf located at a height H, when it reaches the edge and falls to the ground. During the fall, it moves at constant velocity v₀ in the x-axis (u.r.m.) and it moves in free fall along the y-axis (u.a.r.m.) due to the action of the gravity. Initially, the velocity in this y-axis is 0 (v_y = 0) and increases as the projectile descends.
Notice the projections of the motion in the axes and verify that they coincide with the motions that we have described (u.r.m. and u.a.r.m.)

Horizontal launch is the composition of a uniform rectilinear motion (horizontal urm) and a uniformly accelerated rectilinear motion of free fall (vertical uarm). The moving object in this kind of motion is often referred to as projectile, or horizontally launched projectile.

Equations

The equations for horizontal launch are:

The equations for the u.r.m. for the x-axis

$x = x_{0} + v_{x} \cdot t$
The equations of u.a.r.m. for the y-axis

$v_{y} = v_{0 y} + a_{y} \cdot t$

$y = y_{0} + v_{0 y} \cdot t + \frac{1}{2} \cdot a_{y} \cdot t^{2}$

Since, as stated above, the velocity forms an angle α with the horizontal, the components x and y are determined by using the most common trigonometric relationships:

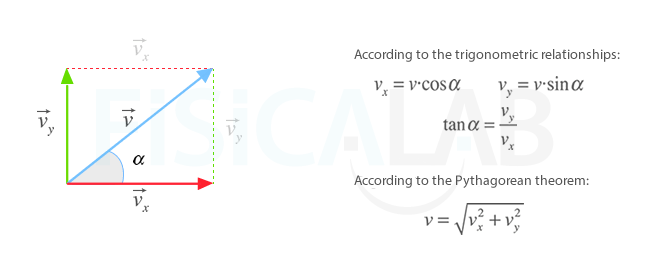
Decomposition of the velocity vector

Any vector, including the velocity, can be broken down is in 2 vectors, v_x and v_y, that have the same directions as the Cartesian axes. The magnitude of both vectors can be calculated from the angle that the vector forms with the horizontal through the expressions shown in the figure.

Finally, taking into consideration what we previously stated, that y₀ = H , x₀ = 0 and a_y = -g, we can rewrite the formulas as they are shown in the following table. These are the final expressions for the calculation of a horizontally launched projectile kinematic magnitudes:

	Position (m)	Velocity (m/s)	Acceleration (m/s²)
Horizontal Axis	$x = x_{0} + v \cdot t$	$v_{x} = v_{0 x} = cte$	$a_{x} = 0$
Vertical Axis	$y = H - \frac{1}{2} g t^{2}$	$v_{y} = - g \cdot t$	$a_{y} = - g$

Experiment and Learn

Data
g = 9.8 m/s² | | |

Horizontal launched projectile

The blue ball in the figure represents a body suspended above the ground. You can drag it up to the initial height H that you want and select the initial velocity (v₀) with which it will be horizontally launched. The gray line represents the trajectory that it will describe with your selected values.

Then press the Play button. Drag the time and observe how its position (x and y) and its velocity (v_x and v_y) are calculated at every moment of its descent toward the ground.

Verify that the projection of the body in the y-axis (green) experiences free fall motion and on the x-axis (red) it describes a uniform rectilinear motion.

Equation of position and trajectory in horizontal launched projectile

The equation of position of a body helps us to determine at what point it is in each moment in time. In the case of a body that is moving in two dimensions, remember that, generically, displacement is described by:

\vec{r} (t) = x (t) \vec{i} + y (t) \vec{j}

Substituting in the previous expressions of the position in the horizontal axis (u.r.m.) and on the vertical axis (u.a.r.m.) in the generic equation of position, we can get to the expression of the equation of position for a horizontal launched projectile.

The equation of position for a horizontal launched projectile is given by:

$\vec{r} = (x_{0} + v \cdot t) \cdot \vec{i} + (y_{0} - \frac{1}{2} \cdot g \cdot t^{2}) \cdot \vec{j}$

On the other hand, to determine the trajectory that the body follows, i.e., its trajectory equation, we can combine the previous equations to eliminate t, leaving:

$y = y_{0} - \frac{1}{2 \cdot {v_{0}}^{2}} \cdot g \cdot x^{2} = y_{0} - k \cdot x^{2}$

Where $k = \frac{1}{2 \cdot {v_{0}}^{2}} \cdot g$ is constant throughout the trajectory.

Example

A tennis ball located 2 m height is hit by a player with his racket. The ball shoots out horizontally with a velocity of 30 m/s. Answer the following questions:

a) How long does the ball takes to hit the ground?
b) What is the angle of the velocity vector with the x-axis at the time the ball reaches the ground?
c) If before being hit, the ball is 5 meters away from the net, how high does the ball pass above the net?

Solution

Concept and representation

Equations

Equation of position and trajectory in horizontal launched projectile

Now... ¡Test yourself!

Related sections

Site

Contact form

Follow us

Horizontal Launch

Ayúdanos a mantenernos en órbita

¿Nuestros contenidos te están resultando de utilidad?

Concept and representation

Equations

Equation of position and trajectory in horizontal launched projectile

Now... ¡Test yourself!

Related sections