Instantaneous Velocity

The everyday concept of velocity arises when we consider how quick or slow a body is moving. Somehow we relate the displacement of the body with the time invested in it. In this section, we are going to specify what is physical velocity, also known as instantaneous velocity, or simply, velocity. To understand this well, we recommend that you previously read the paragraph in which we present average velocity.

Instantaneous velocity

The physical velocity of a body in a point, or instantaneous velocity, is the velocity the body has at a specific time in a particular point of its trajectory.

Instantaneous velocity, or simply velocity, is defined as the limit of the average velocity when the time change approaches zero. It is also defined as the derivative of the position vector with respect to time. Its expression is given by:

\vec{v} = \lim_{∆ t \to 0} {\vec{v}}_{a v g} = \lim_{∆ t \to 0} \frac{∆ \vec{r}}{∆ t} = \frac{d \vec{r}}{d t}

where:

$\vec{v}$ : Instantaneous velocity vector. Its unit in the International System is meter per second ( m/s )
${\vec{v}}_{a v g}$ : Average velocity vector. Its unit of measurement in the International System is the meter per second ( m/s )
$∆ \bar{r}$ : Displacement Vector. Its unit of measurement in the International System is the meter ( m )
$∆ t$ : Interval of time that tends to zero, that is, an infinitely small interval. Its unit in the International System is the second ( s )

Velocity is a vector magnitude. Its dimensional equation is given by [v]=[L][T]^-1

How is the expression of the instantaneous velocity obtained?

To define the concept of instantaneous velocity with precision we start with the concept of average velocity, which we have already studied, and we are going to help ourselves with the graph in the figure.

deduction of velocity in a given point

The procedure to define the instantaneous velocity or, simply, the velocity of a body at a point A, consists in calculating the average velocity between A and a point as close to A as possible. This is the same as calculating the average velocity in an interval of time as small as possible. In the graph, you can see the position vector of the point A and of the rest of points B, C and D. These are ${\vec{r}}_{A}$ , ${\vec{r}}_{B}$ , ${\vec{r}}_{C}$ and ${\vec{r}}_{D}$ respectively. The displacement vectors between A and each of the points B, C and D are also represented. These are ${\vec{r}}_{A}$ , ${\vec{r}}_{B}$ , ${\vec{r}}_{C}$ and ${\vec{r}}_{D}$ respectively. As you can see in the above graph, as the second point gets closer to A the displacement vector get closer to becoming tangent to the trajectory at point A and its magnitude approaches the value of the distance traveled over the trajectory.

Experiment and Learn

Proximity of the distance traveled and the displacement

The graph shows the trajectory followed by a body and its position at two different times.

Drag both positions and observe the values of the displacement and of distance traveled.

What happens when they are very close? The distance traveled is practically equal to the magnitude of the displacement vector. In particular, if the elapsed time between the two positions approaches 0, these become exactly the same. This approximation is what is used to calculate the velocity in a moment in time.

It is more common to find the velocity vector written by means of its Cartesian components resulting in:

velocity vector in 3 dimensional Cartesian coordinates:

$\vec{v} = v_{x} \vec{i} + v_{y} \vec{j} + v_{z} \vec{j} = (\lim_{∆ t \to 0} \frac{∆ x}{∆ t}) \vec{i} + (\lim_{∆ t \to 0} \frac{∆ y}{∆ t}) \vec{j} + (\lim_{∆ t \to 0} \frac{∆ z}{∆ t}) \vec{j} = \frac{d x}{d t} \vec{i} + \frac{d y}{d t} \vec{j} + \frac{d z}{d t} \vec{j}$
velocity vector in 2 dimensional Cartesian coordinates:

$\vec{v} = v_{x} \vec{i} + v_{y} \vec{j} = (\lim_{∆ t \to 0} \frac{∆ x}{∆ t}) \vec{i} + (\lim_{∆ t \to 0} \frac{∆ y}{∆ t}) \vec{j} = \frac{d x}{d t} \vec{i} + \frac{d y}{d t} \vec{j}$

It is also possible that, like with any other vector, you will find it written as a function of its magnitude. To do this, simply multiply the magnitude of the velocity vector by the unit vector with the same direction as $\vec{v}$ , and that we will call ${\vec{u}}_{t}$ because it is tangent to the trajectory.

$\vec{v} = v \cdot {\vec{u}}_{t}$

As you can see, the instantaneous velocity is a vector magnitude that satisfies the following:

Its magnitude may be expressed:
- As a function of the displacement vector or as a function of the distance traveled:
  
  $|\vec{v}| = \lim_{∆ t \to 0} |{\vec{v}}_{a v g}| = \lim_{∆ t \to 0} \frac{|∆ \vec{r}|}{∆ t} = \lim_{∆ t \to 0} \frac{∆ s}{∆ t}$
- When the velocity vector is expressed using Cartesian coordinates in 3 dimensions:
  
  $|\vec{v}| = \sqrt{v_{x}^{2} + v_{y}^{2} + v_{z}^{2}}$
- When the velocity vector is expressed using Cartesian coordinates in 2 dimensions:
  
  $|\vec{v}| = \sqrt{v_{x}^{2} + v_{y}^{2}}$
Its direction is tangent to the trajectory (it touches it at only one point).
Its direction is the same as the displacement vector

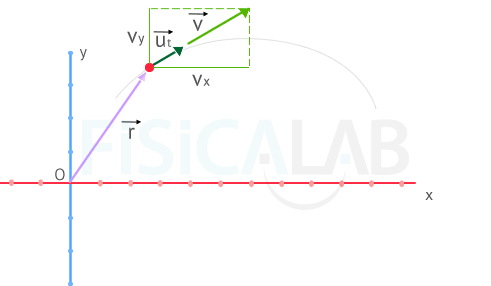
Cartesian components of the velocity vector

Conclusion

In this section, we have defined the concept of instantaneous velocity based on average velocity, we have studied its magnitude and its direction. Even though we have considered different points of view and different expressions for the velocity vector and its magnitude, normally, you will calculate the velocity as the derivative of the position vector with respect to time.

Example

If a body moves according to the following equation:

$\vec{r (t)} = (4 \cdot t + t^{2}) \cdot \vec{i} + 4 \cdot t \cdot \vec{j} m$

Calculate its instantaneous velocity at time t=1 s.

Solution