Ayúdanos a mantenernos en órbita
¿Nuestros contenidos te están resultando de utilidad?
Con un pequeño gesto podremos mantenernos en órbita. Regístrate para acceder a contenidos y funcionalidad exclusiva. Además, con tu ayuda podremos continuar ofreciendo nuestros servicios de manera gratuita para miles de estudiantes en todo el mundo. Te ofrecemos:
- Un campus virtual orientado a la gamificación
- Nuevos contenidos premium
- Nuevas simulaciones
- Acceso prioritario a nuestro plantel de profesores de física y matemáticas
Distance traveled
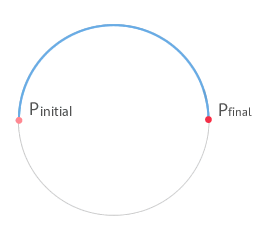
Imagine we are traveling by car from Santurce to Bilbao. Before leaving we reset the odometer to zero. As we move forward on our way the odometer reading will increase its value until we arrive to Bilbao, where the odometer will show the distance traveled between the two cities (for example 22 km). The length of road, measured over the trajectory, is called distance traveled, or simply distance. This measurement is a scalar, and like any length, its unit in the International System (S.I.) is the meter (m).
The distance traveled,
Distance Traveled
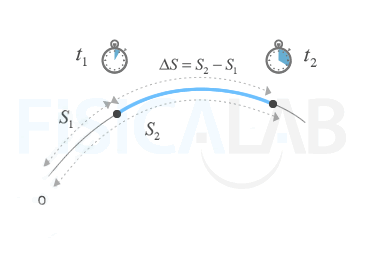
The distance traveled by a body, between two positions, is the length of the trajectory between those two positions, or what is the same, it is the difference of the distance traveled up to the last position (S2) minus the distance traveled in the previous stretch (S1)
In general, the calculation of the distance traveled is equivalent to the calculation of the length of the trajectory curve. This calculation is not immediate and requires mathematical tools which exceed the level in which we find ourselves. However, it is important to remember that, in the case of circular trajectories, the calculation of the distance traveled is equivalent to the calculation of the length of the circumference arc and that is given by:
Where:
- L : Arc length
- r : Radius of the arc
Finally, remember that the distance traveled is always positive, since the length of the curve described by a moving body will always be a scalar greater than or equal to zero.
A body moves between any two instants of time following a circular path with a radius of 5 meter, as you can see in the figure.
Determine:
- The displacement vector of the body and the distance traveled, assuming the origin of the system of reference is located at the starting point of the motion
- The displacement vector of the body and the distance traveled, assuming the origin of the system of reference is in the center of the semicircle