Ayúdanos a mantenernos en órbita
¿Nuestros contenidos te están resultando de utilidad?
Con un pequeño gesto podremos mantenernos en órbita. Regístrate para acceder a contenidos y funcionalidad exclusiva. Además, con tu ayuda podremos continuar ofreciendo nuestros servicios de manera gratuita para miles de estudiantes en todo el mundo. Te ofrecemos:
- Un campus virtual orientado a la gamificación
- Nuevos contenidos premium
- Nuevas simulaciones
- Acceso prioritario a nuestro plantel de profesores de física y matemáticas
Among all constant acceleration motions that occur in the nature, there are two of particular interest: free fall and vertical launch. In this section, we will study free-falling objects. Both, free fall and vertical launch, are governed by the equations of the uniformly accelerated rectilinear motion (u.a.r.m.) or constant acceleration motion:
Free fall
In free fall, an object falls vertically from a certain height H disregarding any kind of friction with the air or any other obstacle. It is a uniformly accelerated rectilinear motion or constant acceleration motion in which the acceleration is gravity. On the Earth surface, the acceleration of the gravity can be considered constant, and directed downwards. It is designated by the letter g and its value is 9.8 m/s2 (sometimes it is approximated to 10 m/s2).
To study free fall motion, normally, we will use a system of reference whose origin of coordinates is at the bottom of the y-axis and we will consider the upward direction as positive, as can be seen in the figure:
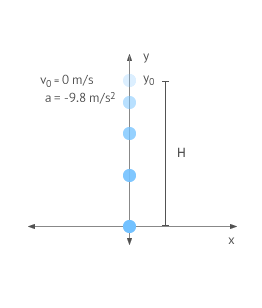
System of Reference in Free Fall
When solving this type of problems, it is customary to use the system of reference in the figure. The body is always on the positive y-axis and its initial position is y0=H, its velocity is 0 m/s (since the body is at rest) and its acceleration is constant and equal to the gravity, but with negative sign because the direction of motion is opposite to that of the y-axis. Keep in mind that the velocity values obtained will also be negative.
So, we get:
Free fall is a constant acceleration motion or uniformly accelerated rectilinear motion (u.a.r.m.) in which a body is dropped vertically from a certain height and does not encounter any obstacle in its way. The free fall equations are:
Where:
- y: Final position of the body. Its unit in the International System (SI) is the meter (m)
- v: Final velocity of the body. Its unit in the International System (SI) is the meter per second (m/s)
- a: The acceleration of the body while in motion. Its unit in the International System (SI) is the meter per second squared(m/s2)
- t: Time spent on the motion. Its unit in the International System (SI) is the second (s)
- H: Height from which the body falls. It is a measurement of length and therefore is measured in meters
- g: Value of the gravitational acceleration which on Earth surface can be considered equal to 9.8 m/s2
If you understand the formulas that we have seen so far, you may be wondering Where is mass in these formulas?. Common sense tells us that a heavy object, such as a hammer, should fall faster than a light object, for example a feather. However, common sense is wrong on this occasion. The fact is that if both, the hammer and feather, were in a vacuum, they would fall at the same velocity. If they are not in a vacuum then the air will resist the fall these bodies, its effect more evident on the lighter feather, which will take longer to get to the ground.
If you are not convinced of what we just inferred, watch the following video in which the astronaut David Scott, Commander of the Apollo 15 mission, drops a hammer and a feather on the Moon surface, where there is no air to resist the fall of the objects: