The constant velocity motion, also known as uniform rectilinear motion (u.r.m.), is the one with constant velocity, i.e., the trajectory is a straight line and the speed is constant. In this section we are going to explain:
Definition of constant velocity motion
While finding rectilinear uniform motion or constant velocity motion in nature is quite rare, it is the easiest to study motion and it will be useful in studying other more complex motions. The uniform rectilinear motion has the following properties:
- The acceleration is zero (a=0) because neither the magnitude nor the direction change
- On the other hand, the initial, average and instantaneous velocities have the same values at all times
A body has constant velocity motion or uniform rectilinear motion when its trajectory is a straight line and its velocity is constant. This implies that it covers equal distances in equal times.
Equations of constant velocity motion
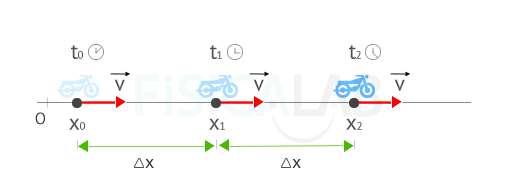
Rectilinear and Uniform Motion
Equal times are spent in traveling equal distances. The average speed is constant and equal to the velocity magnitude.
The equations of constant velocity motion are:
Where:
- x, x0: Position of the body at a given time (x) and at the initial time (x0). Its unit in the International System (S.I.) is the meter (m)
- v,v0: Velocity of the body at a given time (v) and at the initial time (v0). Its unit in the International System (S.I.) is meter per second (m/s)
- a: Acceleration of the body. Its unit of measure in the International System (S.I.) is the meter per second squared (m/s2)
To deduce the equations of uniform rectilinear motion u.r.m. it should be should be taken into consideration that:
- Average velocity coincides with instantaneous velocity
- There is no acceleration
With these restrictions, we get:

