In physics, we say that a body has acceleration when there is a change in the velocity vector, either in magnitude or direction. In this section, we are going to study the concept of average acceleration, which represent the variation in velocity that, on average, takes place in a time interval.
Average Acceleration
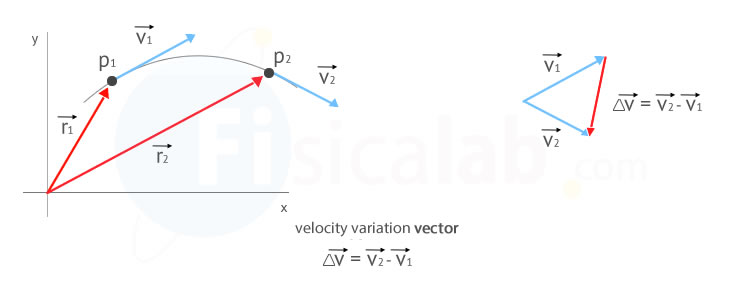
Average acceleration between two points P1 and P2 is defined as the ratio of the variation of the velocity and the time used to complete the motion between both points:
where:
- t1,t2: Initial and final times respectively
Additionally, the average acceleration vector satisfies the following:
- The dimensional equation of the average acceleration is [aa] = [LT-2]
- The unit of measurement in the International System (S.I.) of the acceleration is meter per second squared (m/s2). A body with a 1 m/s2 acceleration changes its velocity by 1 meter/second every second
- Its magnitude (the "size" of the vector) is equal to the magnitude of the velocity variation vector divided by the elapsed time
- Its direction is the same as the direction of the velocity variation vector
It is important to remember that motion, which is colloquially called "braking", is also considered accelerated motion in physics, because in the end, the velocity vector is changing (specifically deceasing its magnitude).

