In physics, we say that a body has acceleration when there is a change in the velocity vector, either in magnitude or direction. In previous sections, we have seen that if this change occurs during an interval of time it refers to the average acceleration in the interval and if it occurs in an instant of time it refers to the instantaneous acceleration. In this section, we are going to study the components of the acceleration according to the effect on the velocity.
Concept of intrinsic components
In previous sections, we have defined acceleration as a change in the velocity vector over time. We have said that the velocity vector can change in magnitude or direction. Thus, two effects of the acceleration are clearly observed:
- The variation of the velocity magnitude (speed)
- The variation of the velocity direction
To study these effects more clearly, we use an instrinsic coordinate system for every point of the trajectory, as you can see in the figure.
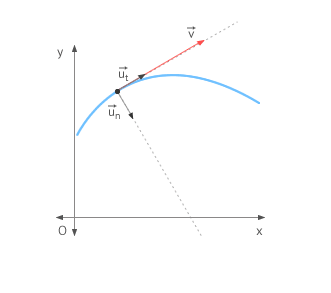
Intrinsic coordinate system
It is established for each point of the trajectory. One of its axis is tangent to the trajectory at that point and its positive direction correspond to the direction of the velocity. The other axis is perpendicular (normal) to the curve at the point and its positive direction is towards the center of curvature.
The intrinsic coordinate system for each point of the trajectory is defined as a system of reference formed by two axes:
- Tangent axis: its direction is tangent to the trajectory and is positive in the same direction than the velocity at that point. It is defined by the unit vector
- Normal axis: it is perpendicular to the trajectory and is positive toward the center of curvature of the trajectory. It is defined by the unit vector
This reference system is used to "observe" the changes in the magnitude and direction of the velocity vector.
The intrinsic components of acceleration are defined as the breakdown of the acceleration vector in its intrinsic axes components.
- The component projected onto the tangent axis is called tangential component and is responsible for the change of the magnitude of the velocity.
- The component projected onto the normal axis is called normal or centripetal component and is responsible for the change in the direction of the velocity.
The acceleration as a function of its components can be expressed in the following way:
Where:
As you can see in the following figure, since the axes are perpendicular to each other, the magnitude of the acceleration can be calculated as:
It is important to realize that, regardless of whether the motion is in two or three dimensions the magnitude of the acceleration vector as a function of its intrinsic components has no more than two variables: the tangential acceleration, that corresponds to the tangent axis and the normal acceleration, that corresponds to the normal axis.
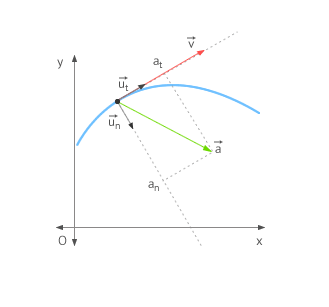
Intrinsic components of acceleration
They are obtained by breaking down of the acceleration vector in two vectors, each located on one axis of the intrinsic system of reference. Regardless of whether the motion is in two or three dimensions there is only two intrinsic components

