A body performs a uniform circular motion (u.c.m.) when its trajectory is a circumference and its angular velocity is constant. In this section, we are going to study the following graphs:
U.C.M. Graphs
Angular position-time (φ-t) graph
The angular position–time graph (φ–t) of a uniform circular motion (u.c.m.). represents time on the horizontal axis (t–axis) and angular position on the vertical axis (φ-axis). The angular position, φ, measured in radians according to the units of the international system (S.I.), increases (or decreases) in a uniform manner with the passage of time. We can distinguish two cases, according to whether the angular velocity is positive or negative:
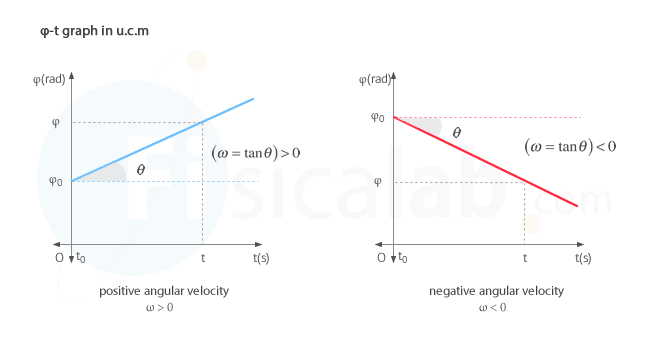
From the angle α, we can get the angular velocity ω. To do it just remember that in a right triangle the tangent of each of its angles is defined as the opposite cathetus divided by the adjacent one:
The value of the slope is the value of the angular velocity ω. So, the greater the slope of the straight line, the higher angular velocity ω of the body.
Angular velocity - time (ω-t) graph
The angular velocity-time graph (ω–t) of a uniform circular motion (u.c.m.) shows that the angular velocity ω, measured in radians per second (rad/s) according to the international system (S.I.), remains constant over time. Again, we can distinguish two cases:
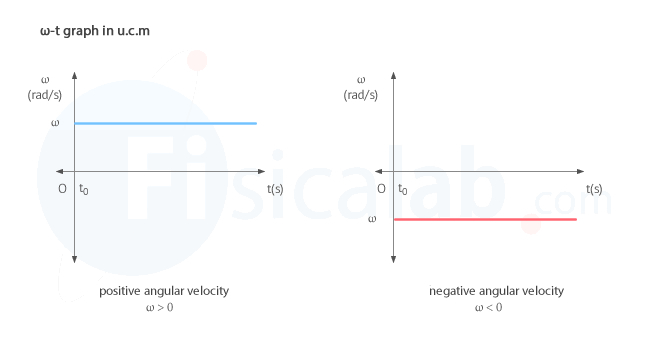
Notice that the area under the curve ω between two instants of time is the angular distance traveled, that is, the angle covered: ∆φ = φ - φ0).

In this case, it is just the calculation of said area, since it is a rectangle. But, do you know what mathematical tool enables the calculation of the area under a curve, whatever its form?
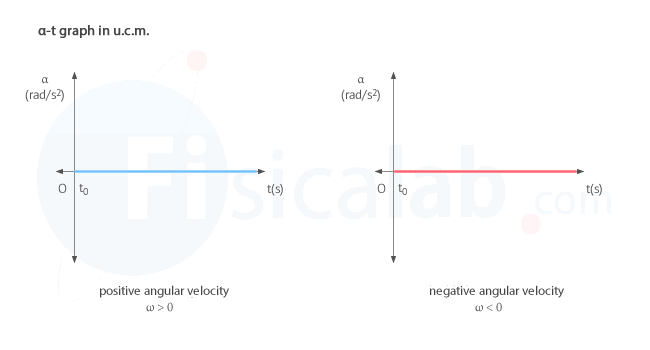
Angular acceleration - time (α-t) graph
The angular acceleration-time graph (α-t) of a uniform circular motion (u.c.m.) shows that the angular acceleration, measured in the international system (S.I.) in radians per second squared (rad/s2), is zero at all times. In this case, whether the velocity of the body is considered to be positive or negative, there is only one possibility, as illustrated in the figure: