Constant Acceleration Motion Graphs

The uniformly accelerated rectilinear motion (u.a.r.m.), also known as constant acceleration motion, is a rectilinear motion that has a constant acceleration, which is different from zero. In this section we are going to study:

• Graph position-time
• Graph velocity-time
• Graph acceleration-time

Constant acceleration motion graphs

Position-time (x-t) graph

$$\boxed{x=x_0+v_{0}t+\frac{1}{2}a{t}^2}$$

The graph position-time (x-t) of a constant acceleration motion, or uniformly accelerated rectilinear motion (u.a.r.m.), represents time on the horizontal axis (t-axis) and position on the vertical axis (x-axis). Observe as the position (normally the x-coordinate) increases (or decreases) uniformly with time. This happens because as time passes, the magnitude of the velocity varies. We can distinguish two cases, when the velocity is positive or when it is negative:

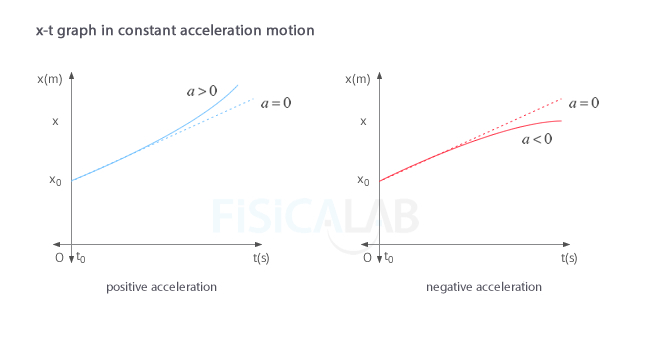
Velocity-time (v-t) graph

$$\boxed{v=v_0+a\cdot t}$$

The graph velocity-time (v-t) of a constant acceleration motion, or uniformly accelerated rectilinear motion (u.a.r.m.), represents time on the horizontal axis (t-axis) and velocity on the vertical axis (x-axis). Observe as the velocity increases (or decreases) uniformly with the passage of time. This happens as the result of the acceleration. Again, we can distinguish two cases:

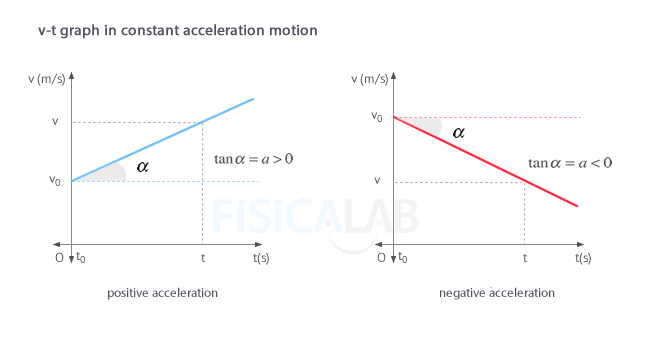
We can get the velocity from the angle α. To do it just remember that in a right triangle the tangent of each of its angles is defined as the opposite side (cathetus) divided by the adjacent one:

$$\tan \alpha =\frac{\text{opposite side}}{\text{adjacent side}}=\frac{∆v}{∆t}=\frac{v-v_0}{t}=a$$

The value of the slope is the magnitude of the acceleration. Therefore, the greater the slope of the straight line, the higher the acceleration of the body.

Notice that the area under the curve v between two instants of time, numerically matches the distance traveled. Could you tell why?

The area under the curve can be calculated as the area of the rectangleo S₁ that would correspond to a uniform rectilinear motion (u.r.m.) to which we will add the area of the triangle S₂:

$$∆x=x-x_0=S_1+S_2\stackrel{1}{\overbrace{=}}{v}_{0}t+\frac{\left(v-v_0\right)t}{2}\stackrel{2}{\overbrace{=}}{v}_{0}t+\frac{1}{2}a{t}^2$$

Where have we applied:

1. $\left\{\begin{array}{c}{S}_1=v_{0}t\\ S_2=\frac{S_{\text{rectangle}}}{2}=\frac{\left(v-v_0\right)t}{2}\end{array}\right.$
2. $v-v_0=at$

Acceleration time (a-t) graph

$$\boxed{a=\text{cst}}$$

The graph acceleration-time (a-t) of a constant acceleration motion, or uniformly accelerated rectilinear motion (u.a.r.m.), shows that the acceleration remains constant over time. It is the average acceleration, which in the case of u.a.r.m. is the same as the instantaneous acceleration. Again, we can distinguish two cases:

Notice that the area under the curve, enclosed between two instants of time, numerically matches the experienced increase of velocity. Do you know why?