When a body is moving in a straight trajectory, we can simplify the vector magnitudes associated with the motion and change them into simple numbers, scalars, with a sign to indicate the direction the magnitude would have. In this section, we are going to study:
- The sign convention in rectilinear motion
- The main characteristics of the rectilinear motion that allow us to use this convention
- How to choose the reference frame adequately
Sing convention in rectilinear motions
When a body moves along a straight line it is said that it has rectilinear motion and it shows a series of properties that will allow us to study it in a simpler way, using scalar magnitudes instead of vectors and following an adequate sign convention or criterion
Rectilinear motion is the one whose trajectory is a straight line. In rectilinear motion, we can treat the kinematic vector magnitudes as if they were the scalar magnitudes x, v and a. The sign convention normally used is summarized in the following illustration.

Sign Convention
The sign of the position of the body is considered the same as that of the half axis (positive or negative half axis) that contains it. The velocity is considered to have a sign equal to the sign of the direction of the motion in the half axis in which it moves.
This convention is also valid for other vector magnitudes like force or linear momentum.
Characteristics of rectilinear motion
The main characteristics of rectilinear motion are the following:
- Its trajectory is a straight line
- It does not have normal (centripetal) acceleration, which, remember, is responsible for the change of the direction of the motion. The only acceleration present is tangential acceleration, which is responsible for the change of the velocity magnitude
-
If the system of reference is chosen so as to make one of the axes match the direction of the movement, the kinematic magnitudes position vector
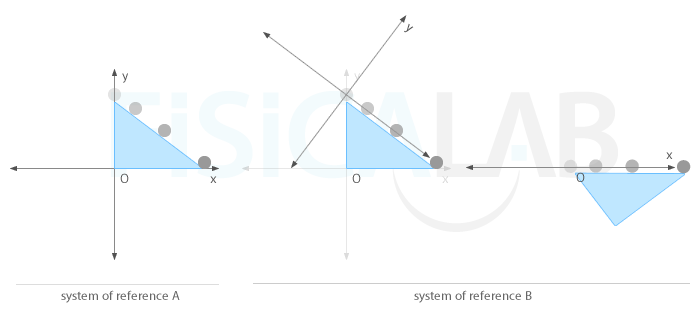
Choice of the system of reference
Choosing the proper reference system can greatly simplify the study of motion. For example, in the system of reference A, the motion takes place in two dimensions (the position of the body is given by two values, x and y) while in B it takes place in one dimension (to determine its position it is enough to know the value of x). The study of motion in one dimension tends to be simpler than in multiple dimensions.
- The position of the body is defined by its coordinates:
-
X-coordinate, in the case of horizontal movements. Normally the following convention of signs for the position is followed: If the body is found to the right of the origin, the coordinate is positive. If it is on the left side, the coordinate is negative.
Equation of position in horizontal rectilinear motion: -
Y-coordinate, in the case of vertical movements. Normally the following convention of signs for the position is followed: If the body is above the origin, the y-coordinate is positive. If it is below, the coordinate is negative. Equation of position in vertical rectilinear motion:
-
-
The velocity of the body is defined by the scalar v.
-
Its value is given by the same expression in both, the x and the y axis:
- Sign convention for velocity is normally as follows:
- Velocity is positive when the body moves in the positive direction of axis
- Velocity is negative when the body moves in the negative direction of the axis
- It is usual the use of the term speed to refer to both, velocity and speed. Actually, speed in the case of rectilinear motion, is the magnitude of v
-
- Acceleration, which is tangential acceleration, is defined by the scalar a.
-
Its value is given by the same expression, both in the x and the y axis we have:
- The sign convention for acceleration is typically as follows::
- Acceleration is positive when the body moves in the positive direction of axis
- Acceleration is negative when the body moves in the negative direction of the axis
-
The following images illustrate the previous ideas. In the first one, the motion of the body is studied using vectors. In the second one, their scalar magnitudes are used instead, based on the adopted conventions.


