Position Vector

In physics, the position, the position vector or the location vector of a body with respect to a coordinate system is defined as the vector that links the location of the body with the origin of the coordinate system. In Cartesian coordinates, it is expressed as:

\vec{r} = x \vec{i} + y \vec{j} + z \vec{k}

Where:

$\vec{r}$ : Is the position vector
x, y, z : Are the coordinates of the position vector
$\vec{i}, \vec{j}, \vec{k}$ : Are the unit vectors in the directions of axes OX, OY and OZ respectively.

The unit of measurement for position in the International System is meter [m]. Like all vectors, the position vector in physics has direction and magnitude (also known as size, modulus or length of the vector). The magnitude of the position vector is the distance of the body to the origin of the reference system. To calculate it you can use the following formula:

|\vec{r}| = \sqrt{x^{2} + y^{2} + z^{2}}

For those problems where you are working in fewer dimensions, you can simplify the previous formula by eliminating unnecessary terms. This way, the position equation:

In two dimensions becomes $\vec{r} = x \vec{i} + y \vec{j} + z \vec{k} = x \vec{i} + y \vec{j}$ ,and its magnitude $|\vec{r}| = \sqrt{x^{2} + y^{2} + z^{2}} = \sqrt{x^{2} + y^{2}}$ , since z=0
In one dimension becomes $\vec{r} = x \vec{i} + y \vec{j} + z \vec{k} = x \vec{i}$ , and its magnitude $|\vec{r}| = \sqrt{x^{2} + y^{2} + z^{2}} = \sqrt{x^{2}} = x$ , since y=0 and z=0

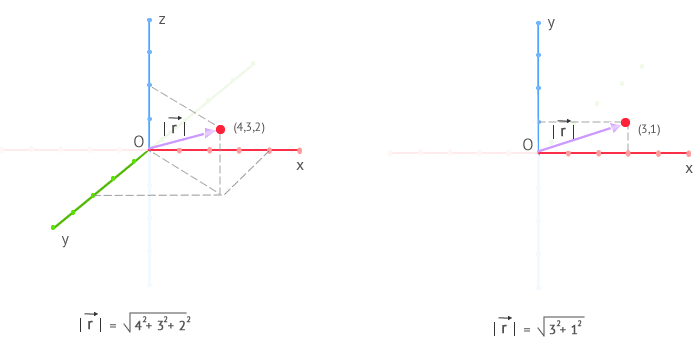
We have represented a position vector in three dimensions (left) and another in two dimensions (right) in the following figure:

Experiment and Learn

Position vector and its magnitude

Slide the body within the coordinate system and observe how the magnitude is as as the coordinates and direction of its position vector change.
Notice that as the body approaches the origin of coordinates (0,0) the modulus of the vector, which is expressed as | $\vec{r}$ |, decreases. What happens if you move it away? , is reduced. What if you move it away?

NOTE: The dotted line is not usually drawn, we show it here so you can see more clearly the direction of the vector.

Formulas
$\vec{r}$ = · $\vec{i}$ · $\vec{j}$ m
$|\vec{r}|$ = m

Example

Find the position vector and its magnitude for the following points:

a) P₁ (-1,2)
b) P₂ (-3,4)

Solution

Position Vector

Now... ¡Test yourself!

Related sections

Site

Contact form

Follow us

Position Vector

Ayúdanos a mantenernos en órbita

¿Nuestros contenidos te están resultando de utilidad?

Position Vector

Now... ¡Test yourself!

Related sections