In physics, we say that a body has acceleration when there is a change in the velocity vector, either in magnitude or direction, which we already saw in the section dedicated to the concept of acceleration. In this section, we are going to study the instantaneous acceleration, which represents the variation of velocity taking place at a specific time.
Instantaneous acceleration
The instantaneous acceleration of a body is the acceleration the body has at a particular time, at a specific point of its trajectory. To define the concept of instantaneous acceleration with precision we must begin with the average acceleration in an interval and make it infinitely small (
The instantaneous acceleration, or simply acceleration, is defined as the limit of the average acceleration when the interval of time considered approaches 0. It is also defined in a similar manner as the derivative of velocity with respect to time. It is given by the expression:
where:
Acceleration is a vector magnitude. The dimensional equation of the instantaneous acceleration is [a] = [L][T]-2 and therefore, its unit of measurement in the International System (S.I.) is the meter per second squared [m/s2].
You can find the acceleration vector expressed by its Cartesian components, thus:
-
acceleration vector in 3-dimensional Cartesian coordinates:
-
acceleration vector in 2-dimensional Cartesian coordinates:
As you can see, the instantaneous acceleration is a vector magnitude that satisfies the following:
- Its magnitude may be expressed:
-
Using Cartesian coordinates in 3 dimensions:
-
Using Cartesian coordinates in 2 dimensions:
-
- Its direction, in general, does not coincide with the velocity vector but it depends on the change experienced by it.
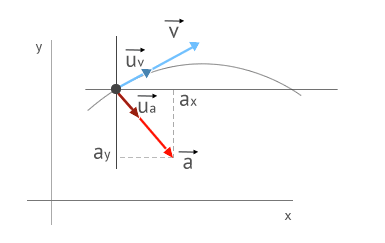
Velocity vector and acceleration vector
Do not confuse the Cartesian components of the acceleration with the intrinsic components, which we will study in subsequent sections. The Cartesian components are, simply put, the decomposition of the acceleration vector in its corresponding components in the Cartesian axes. The intrinsic components result from the breaking down of the acceleration vector in the reference system intrinsic to the motion.
And finally, to point to you that, like with any other vector, you may occasionally find the acceleration vector written in terms of its magnitude. To do this simply multiply the magnitude of the acceleration vector by a unit vector with the same direction as

