Tangential Acceleration

In physics, we say that a body has acceleration when there is a change in the velocity vector, either in magnitude or direction. In previous sections, we have seen that acceleration can be classified, according to the effect that it produces in the velocity, in tangential acceleration (if it changes the magnitude of the velocity vector) and in normal or centripetal acceleration (if it changes its direction). These are the intrinsic components of the acceleration. In this section, we are going to develop the concept of tangential acceleration in more detail.

Tangential acceleration

Previously we have seen that the instantaneous acceleration is the derivative of the velocity with respect to time. On the other hand, we have seen that we can express the velocity vector as the product of its magnitude and a unit vector tangent to the trajectory $\vec{v} = v \cdot {\vec{u}}_{t}$ . If we develop these two ideas, we get:

$\vec{a} = \frac{d \vec{v}}{d t} = \frac{d (v \cdot {\vec{u}}_{t})}{d t} \overset{D(a⋅b)}{\overset{⏞}{=}} \frac{d v}{d t} {\vec{u}}_{t} + v \frac{d {\vec{u}}_{t}}{d t}$

Where we have applied the derivative of a product rule D(ab)=a'b+ab'.

We see that the first term ( $\frac{d \vec{v}}{d t} {\vec{u}}_{t}$ ) is tangential to the trajectory because it is multiplying the unit vector ${\vec{u}}_{t}$ . This term is known as tangential acceleration and is the same as the everyday concept of acceleration, which is the change of the magnitude of the velocity. ,>

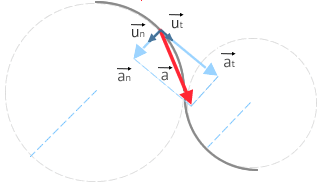
Intrinsic components of the acceleration

Tangential acceleration ( $\vec{a_{t}}$ )| Normal acceleration ( $\vec{a_{n}}$ )

Tangential acceleration measures the rate of change of the velocity magnitude over time. It is given by the expression:

{\vec{a}}_{t} = \frac{d v}{d t} {\vec{u}}_{t}

Where:

${\vec{a}}_{t}$ : Is the tangential acceleration vector
$v$ : Is the magnitude of the velocity vector
${\vec{u}}_{t}$ : Is the unit vector that correspond to the direction of the motion on the tangent axis

The value of the tangential acceleration may be:

Greater than zero (> 0): When the body has accelerated motion, that is, the magnitude of the velocity vector increases with time
Less than zero (<0): When the body has slowing or decelerated motion, that is, the magnitude of the velocity vector decreases with time
Equal to zero (= 0): When the body has uniform motion, that is, the magnitude of the velocity vector remains constant

Example

Knowing that the magnitude of the velocity of a body in S.I. units is:

$v = 7 + 2 \cdot t + 3 \cdot t^{2}$

Calculate the magnitude of the tangential acceleration.

Solution