A projectile is any object that once launched or dropped continues in motion by its own inertia and is influenced only by the downward force of gravity.
Projectile motion, also known as parabolic motion, is an example of composition of motion in two dimensions: an u.r.m. on the horizontal axis and a u.a.r.m. on the vertical axis. In this section, we will study:
- The concept and representation of parabolic motion
- Its equations
- The maximum height a body reaches in parabolic motion
- The time it is in the air
- The range
- The angle of the trajectory
Shall we begin?
Concept and representation
Projectile motion, also known as parabolic motion, consists in launching a body with a velocity that form an angle α with the horizontal. In the following figure, you can see a representation of the situation.
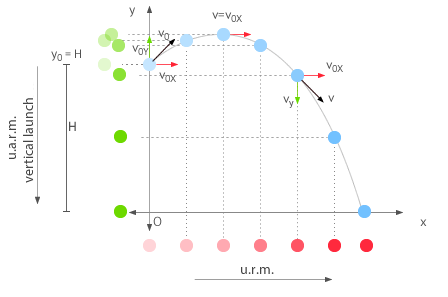
Parabolic Motion
This motion is characteristic of projectiles, moving objects being affected only by gravity. On the x-axis, the body moves at constant velocity v0x (u.r.m.) and in the y-axis with constant acceleration due to gravity (u.a.r.m.).
It is characterized by the fact that at the highest point of the trajectory, the velocity of the body is always v0x (there is no vy).
Projectile motion or parabolic motion is the result of the composition of a uniform rectilinear motion (horizontal urm) and a uniformly accelerated rectilinear motion of launching upward or downward (vertical uarm).
Equations
The equations for projectile motion are:
-
The equations for the u.r.m. on the x-axis
-
The equations for the u.a.r.m. on the y-axis
Since, as we said above, the velocity forms an angle α with the horizontal, the x and y components are determined using the most common trigonometric relationships:
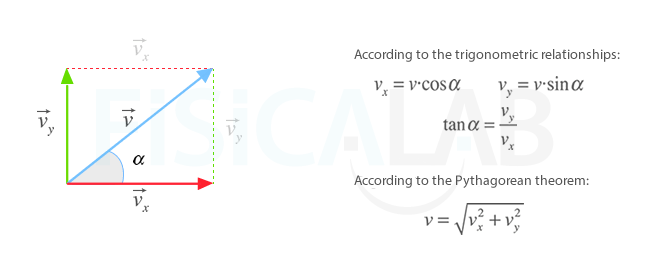
Decomposition of the velocity vector
Any vector, including the velocity, can be broken down is in 2 vectors, vx and vy, that have the same directions as the Cartesian axes. The magnitude of both vectors can be calculated from the angle that the vector forms with the horizontal through the expressions shown in the figure.
Finally, taking into consideration the above said, that y0 = H , x0 = 0, and that ay = -g , , we can rewrite the formulas as are shown in the following list. These are the final expressions for calculating kinematics magnitudes in projectile motion or parabolic motion:
- Position (m)
-
Horizontal axis
-
Vertical axis
-
- Velocity (m/s)
-
Horizontal axis
-
Vertical axis
-
- Acceleration (m/s2)
-
Horizontal axis
-
Vertical axis
-
Equation of position and trajectory in projectile motion
The equation of position of a body helps us to know at what point it is at each instant of time. In the case of a body moving in two dimensions, remember that, generically, it is described by:
Substituting the above expressions of the position on the horizontal axis (u.r.m.) and on the vertical axis (u.a.r.m.) in the generic equation of position, we can get the expression of the equation of position for parabolic motion.
The equation of position of the projectile motion is given by:
On the other hand, to know which trajectory the body follows, that is, its equation of trajectory, we can combine the above equations to eliminate t, getting:
As expected, this is the equation of a parabola.
On the other hand, frequently in exercises, you would be asked for some of the following values.
Maximum height
This value is reached when the velocity in the y-axis, vy , is 0. Starting from the equation of velocity in the y-axis, and making vy = 0, we get the time t that it takes the body in get to this height. From that time, and from the equations of position, we can calculate the distance to the origin in the both axes, the x-axis and y-axis.
Flight time
It is calculated for y = 0, the vertical component of the position. That is, the flight time is the time required for the height to become 0 (the projectile reaches the ground).
Range
It is the maximum horizontal distance, from the starting point of the motion to the point in which the body hits the ground. Once the strong>flight time is obtained, simply substitute in the equation of position of the horizontal component.
Angle of the trajectory
The angle of the trajectory in a given point is the same as the angle that the velocity vector form with the horizontal at that point. To calculate it, we get the components vx and vy and from the trigonometric definition of the tangent of an angle, we calculate α:

