Normal or Centripetal Acceleration

In physics, we say that a body has acceleration when there is a change in the velocity vector, either in magnitude or direction. In previous sections, we have seen that acceleration can be classified, according to the effect that it produces in the velocity, in tangential acceleration (if it changes the magnitude of the velocity vector) and in normal or centripetal acceleration (if it changes its direction). These are the intrinsic components of the acceleration. In this section, we will study normal or centripetal acceleration in more detail.

Normal or centripetal acceleration

Normal or centripetal acceleration measures the changes in the direction of the velocity with time. It is given by the expression:

{\vec{a}}_{n} = \frac{v^{2}}{ρ} {\vec{u}}_{n}

Where:

${\vec{a}}_{n}$ : Is the normal or centripetal acceleration of the body
$v$ : Is the velocity of the body in the point being studied
$ρ$ : Is the radius of curvature. In the case of circular motion, it is same as the radius of the circle

Normal acceleration can be:

=0: In the rectilinear motion, in which the direction remains constant
>0: In the curvilinear motion, in which the direction of the velocity changes

Notice that any trajectory described by a body can be considered as a combination of straight and curved trajectories. The curved portions of the trajectory may also be considered circumference arcs. The following image illustrates this concept

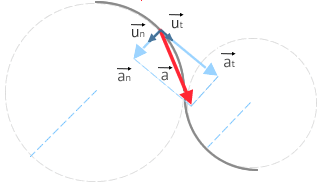
Intrinsic components of the acceleration

Tangential acceleration ( $\vec{a_{t}}$ )| Normal acceleration ( $\vec{a_{n}}$ )

As we can see, the center of curvature at a point of the curved trajectory is the same as the center of the circle that passes through it. The radius of this circle is the radius of curvature at that point.

Demonstration of normal acceleration

Previously, we have seen that the instantaneous acceleration is the derivative of the velocity with respect to time. On the other hand, we have seen that we can express the velocity vector as the product of its magnitude and a unit vector tangent to the trajectory: $\vec{v} = v \cdot {\vec{u}}_{t}$ If we develop these two ideas, we get:

$\vec{a} = \frac{d \vec{v}}{d t} = \frac{d (v \cdot {\vec{u}}_{t})}{d t} \overset{D(a⋅b)}{\overset{⏞}{=}} \frac{d v}{d t} {\vec{u}}_{t} + v \frac{d {\vec{u}}_{t}}{d t}$

Where we have applied the derivative of a product rule D(ab)=a'b+ab'.

We see that the second term is the product of the magnitude of the velocity and the derivative of ${\vec{u}}_{t}$ with respect to time. We can demonstrate that this vector is, actually, normal to the path:

normal acceleration and tangential acceleration

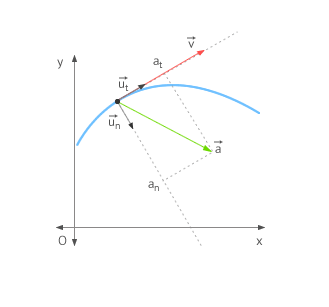
Acceleration components

We express ${\vec{u}}_{t}$ as a function of the generic angle $θ$

${\vec{u}}_{t} = \cos θ \vec{i} + \sin θ \vec{j}$
We apply the chain rule

$\frac{d {\vec{u}}_{t}}{d t} = \frac{d {\vec{u}}_{t}}{d θ} \frac{d θ}{d t} = (- \sin θ \vec{i} + \cos θ \vec{j}) \frac{d θ}{d t} = {\vec{u}}_{n} \frac{d θ}{d t} \overset{θ = s / ρ}{\overset{⏞}{=}} {\vec{u}}_{n} \frac{1}{ρ} \frac{d s}{d t} \overset{s = v t}{\overset{⏞}{=}} \frac{v}{ρ} {\vec{u}}_{n}$
From the previously mentioned we deduce that:

$\vec{a} = \frac{d v}{d t} {\vec{u}}_{t} + v \frac{d {\vec{u}}_{t}}{d t} = \frac{d v}{d t} {\vec{u}}_{t} + v \frac{v}{ρ} {\vec{u}}_{n} = \frac{d v}{d t} {\vec{u}}_{t} + \frac{v^{2}}{ρ} {\vec{u}}_{n}$

The framed term corresponds to the normal or centripetal acceleration and it is responsible for the change of direction of the velocity over time.