Non-Uniform Circular Motion

A body carries out a non-uniform circular motion when its trajectory is a circumference and its angular acceleration is constant. In this section, we are going to study:

• The concept of non-uniform circular motion using its main kinematic magnitudes
• The main features of this kind of motion

Concept of non-uniform circular motion

Your day to day is full of examples of circular motion with constant angular acceleration: you can see it in the motion of the blades when you turn on or turn off a fan, or maybe it can also happen with the tires of a car stopping at a traffic light. Many of the usual u.c.m., before reaching a certain constant angular velocity, they must go through a period in which they are a non-uniform circular motions.

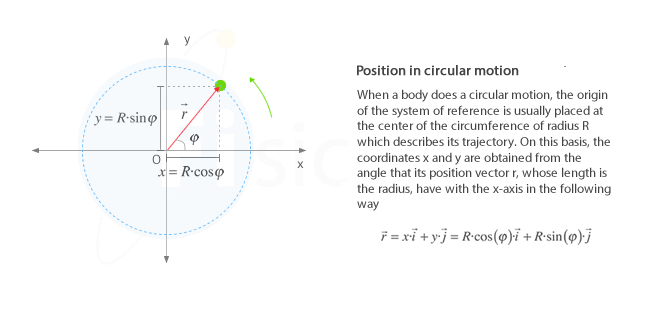
We can describe the position of an element that moves according to a non-uniform circular motion in the same way we did with uniform circular motion. We start by placing the origin of coordinates at the center of the circumference, and knowing its radius R, we can express the position vector as follows:

This way, the position and the rest of the kinematic magnitudes will be defined by the value of φ at each instant.

Characteristics of non-uniform circular motion

Some of the main features of the non-uniform circular motion are the following:

1. The angular acceleration is constant (α = cat)
2. There is tangential acceleration a_t and it is constant. Remember that $a_t=\alpha ·R$ , with R the radius of the motion
3. There is normal or centripetal acceleration a_n which is responsible for the change of direction of the velocity vector. However, it is not constant, but rather depends on the velocity at the point considered. Remember that $a_n=\frac{v^2}{R}={\omega }^2·R$
4. The angular velocity ω increases or decreases uniformly