Uniform Circular Motion (U.C.M.)

 

A body performs a uniform circular motion (u.c.m.) when its trajectory is a circumference and its angular velocity is constant. In this section, we are going to study:

Concept of U.C.M.

Nature and your daily life are full of examples of uniform circular motion (u.c.m.). Earth itself is one of them: it does a full rotation around its axis every 24 hours. Old record players or fans are other good examples of u.c.m.

Uniform circular motion (u.c.m.) is motion with a circular trajectory in which the angular velocity is constant. This implies that the body travels equal angles in equal times. In this motion, the magnitude of the velocity vector does not change but its direction (which is tangent to the trajectory at each point) changes. This means it neither has tangential nor angular acceleration, although it does have normal acceleration.

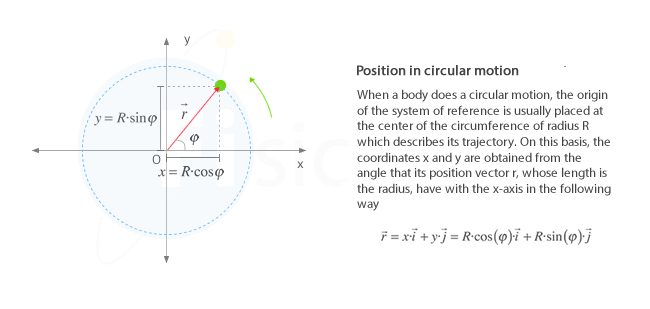
Placing the origin of coordinates at the center of the circumference, and knowing its radius R, we can express the position vector as follows:

r→=x·i→+y·j→=R·cosφ·i→+R·sinφ·j→

This way, the position and the rest of the kinematic magnitudes will be defined by the value of the angle φ at each instant.

Position vector in uniform circular motion

Characteristics of Uniform Circular Motion (U.C.M.)

Some of the main features of the uniform circular motion (u.c.m.) are the following:

  1. The angular velocity is constant (ω = cst)
  2. The velocity vector is tangent to the trajectory at each point and its direction is the same as the direction of the motion. This means that the motion has normal acceleration
  3. Both, the angular acceleration (α) and tangential acceleration (at) are zero, since the speed (the velocity vector magnitude) is constant
  4. There is a period (T), that is the time that the body takes in completing a full rotation. This means that the characteristics of the motion are the same every T seconds. The expression for the calculation of the period is T=2π/ω and it is only valid in the case of uniform circular motion (u.c.m.)
  5. There is a frequency (f), which is the number of complete rotations per second the body gives. Its value is the inverse of the period
Experiment and Learn
 
Data
 
 
 
 
 
Uniform circular motion (u.c.m.)

The graph shows a body doing uniform circular motion.

Drag the value of the speed (magnitude of the velocity vector) to observe how the body moves faster or slower.

Observe the different kinematic magnitudes. Additionally, verify that the velocity vector, in green, is tangent at each point to the trajectory and, on the other hand, the normal acceleration, in red, is responsible for the change in direction of the speed. Its direction always points to the center the circular trajectory and its value (magnitude) depends on the speed of the body.

Example
A body describes a uniform circular motion with a 3 m radius. What is its position vector when its angle is 30º?
Solution

Now... ¡Test yourself!

Related sections

Contents of Uniform Circular Motion (U.C.M.) are closely related to:

Intrinsic Components of Acceleration
Angular Quantities
Equations of Uniform Circular Motion (U.C.M.)
Uniform Circular Motion (U.C.M.) Graphs