The english physicist, mathematician and astronomer Sir Isaac Newton (1642-1727), basen on the studies of Galileo and Descartes, published in 1684 the first great work in Physics: Philosophiæ Naturalis Principia Mathematica, also known as Principia. In the first of the three parts in which the work is divided, he exposes in three laws of motion the relations between forces and their dynamic effects: the laws of motion.
- Newton´s first law or inertia principle.
- Newton´s second law or law of force and acceleration.
- Newton´s third law or law of action and reaction.
During this chapter we are going to study the first of the three laws. In order to this we will see:
- The concept of inertia related to the first law
- The definition of the Newton´s first Law
- Its relation with the linear momentum
- What are the reference and inertial frame systems
Shall we start?
Concept
Since Aristotle´s times was usual to think that to keep in motion a body must act a force continuously on it. Think, for example, of soccer ball that, after being hit and walk a few metres, finally stops. It is very likely that Aristotle didn´t know the curling... or ice hockey since they would have led him to consider his motion theory.
Effectively, as Galileo and Descartes propose, the bodies tend to maintain their motion state. It´s what we know as inertia. Actually, what does bodies to stop is the presence of a force against movement: the frictional force.
So, Newton´s first law gathers the ideas about inertia that Galileo and Descartes had already suggested and he mathematicaly formalised.
Definition
Newton´s first law, also known as Inertia Principle, establishes that a body does not modifies its resting state or motion state either no force is applied on it, either the resultant force applied is absent. That is, it will remain at rest if it was at rest or uniform line movement if it was in motion.
It is deduced from here:
- All bodies are against changing their state of rest or motion and this oppositionis called inertia. The mass of a body , understood this as its matter quantity, it is a quantitative measure of the inertia of a body.
- A body is in equilibrium when the resultant force acting on it is absent.
Differential definition
We can do a more formal definition of this first principle by using derivatives. Do you remember what is the meaning of a derivative in physics? Of course, the derivative of a function told us how this function varied. If we say that, with no external forces, the velocity remains constant in time, what we are saying is that the derivative of the velocity in relation to time is zero, so, there is no variation of velocity regarding time. Therefore, we can express Newton´s first law:
Inertia and Linear Momentum
As we know, the movement of a body is characterised by its quantity of motion or linear momentum, which relates its mass to its velocity. Assumming that the mass of a body remains constant along the movement, this law can be stated as follows:
The linear momentum or quantity of motion of an isolated body remains constant.
It´s the conservation principle of linear momentum on which we talk about in next chapters.
Inertial and non inertial reference frames
In the chapter related to the study of motion we have highlighted the importance of the frame of reference in order to say should a body is in motion or it is not. We can ask a question here: is the Newton´s first law accomplished for any frame of reference?
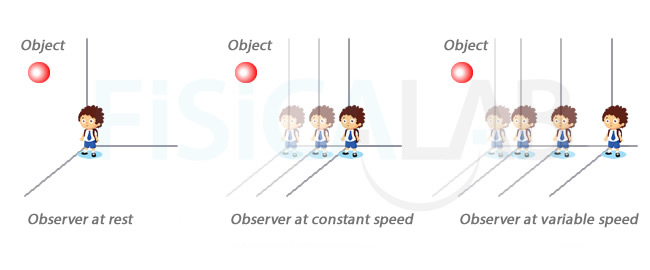
We are going to analyze the three situations to see if they accomplish the Newton´s first law:
- It is obvious that in the first situation the observer, at rest, perceive the object also at rest, so, its linear momentum remains constant. The first observer can affirm that there is no force acting over the body. Newton´s first law is accomplished.
- In the second situation the observer gets away from the body at a constant speed (in u.r.m.). Since he is not able to perceive his own motion, he will perceive the body moving away from him at a constant speed. In any case, he can also affirm that there is no force acting over the body, because the speed used by the body to get away does not vary, so its linear momentum remains constant. We can also say that Newton´s first law is accomplished.
- The third of our observers is the most special. He gets away from the body faster everytime (u.a.r.m.), this will make him perceive the body has acceleration, that is, it varies its speed and so its linear momentum. To accomplish Newton´s first law, the observer must say there is a force acting over the body.
We can see that the two first obervers´observation is different from the third one despite the body´s behaviour is the same... To accomplish the first law, the third observer must insert a fictitious force (since it is not respond to any interaction), which is known as inertial force. This allow us to distinguish clearly two types of frames of reference:
We say that a frame of reference is inertial when it achieves the inertia principle (and in concequence the laws of physics). The frames of reference at rest or at constant speed are inertial reference frames. We say that a frame of reference is non inertial when it does not achieve the inertia principle (and in consequence the laws of physics). The frames of reference with acceleration of any kind are non inertial reference frames.
Observ that on the definition we have made there is an implicit second observer: ourselves. So, we can say: "inertial frames of reference are at rest or at constant speed". Actually we might say "inertial frames of reference are at mutual rest or moves at relative constant speed".
Newton considered the absolute space, a kind of frame of reference at absolute rest about which the concepts "at rest" or "uniform rectilinear motion" would make sense. He would understand that a frame at rest is the one that it is at rest in relation to fixed stars, those are the ones that do not move with respect to each other.
Finally, Newton himself realized that it may not exist any body at absolute rest. Effectively, it is impossible to find in the real world inertial reference frames, since there is always some kind of force acting over the bodies. In any case, its always possible to find a frame of reference in which the issue we are studying can be treated as if we were in an inertial reference frame.