The everyday concept of speed arises when we consider how quick or slow a body moves. Somehow we relate the displacement of the body with the time spent in such displacement. In this section, we are going to define what is meant in physics by average speed and its difference with average velocity.
Average speed
Average speed of a body that moves from point P1 to point P2 is defined as the ratio of the distance traveled and the corresponding elapsed time. It is given by the expression:
where:
- s1 ,s2 : Distance traveled by the body on the trajectory from the beginning of the motion to P1 (s1), and from the beginning of the motion to P2 (s2). The unit of measurement in the International System (S.I.) is the meter (m)
- t1, t2 : Time in which the body is found in the initial point P1 and in the final point P2 respectively. The unit of measurement in the International System (S.I.) is the second (s)
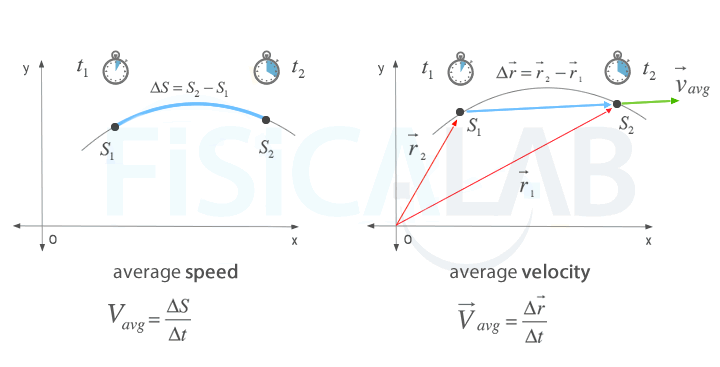
Average speed is a scalar magnitude as opposed to average velocity which is a vector. The unit of measurement in the International System (S.I.) of the average speed is the meter per second (m/s). On the other hand, unlike average velocity, which depended on the vectors of the initial and final positions of the motion, the average speed depends on the distance traveled over the trajectory. Therefore, a body in motion will always have an average speed greater than 0. In general, the

