Statement
Based on the graphs of angular position–time (φ–t), angular velocity–time (ω–t), angular acceleration–time (α–t) of uniform circular motion (u.c.m.) draw the graphs of distance traveled–time (s–t), velocity–time (v–t), tangential acceleration–time (at–t) and normal acceleration–time (an–t). Considering that angular velocity is ω>0.
Solution
Distance traveled – time (s–t) graph in u.c.m.
The distance traveled–time graph (s–t) in uniform circular motion (u.c.m.). represents time on the horizontal axis (t-axis) and distance traveled in the vertical axis (s-axis). Given that, in the statement, we are told that the angular velocity is positive, the angular position will increase evenly with the passage of time and so will the distance traveled, since:
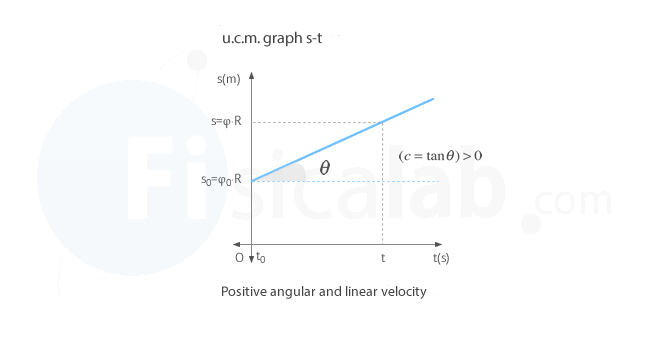
From the angle θ we can get the average speed c. To do it just remember that in a right triangle the tangent of each of its angles is defined as the opposite cathetus divided by the adjacent one:
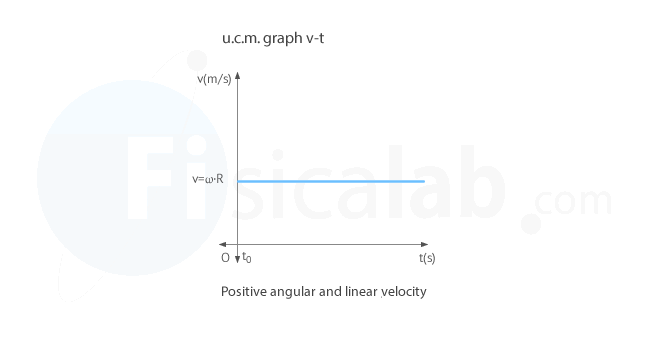
Velocity – time (v–t) graph in u.c.m.
Since velocity is directly proportional to the angular velocity and this last one is constant, the velocity–time graph (v–t) in this type of motion will also be constant over time:
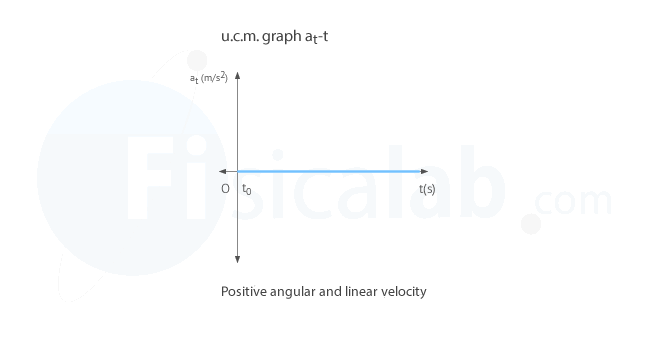
Tangential acceleration – time (at–t) graph in u.c.m.
Since the u.c.m. is a uniform motion, the velocity magnitude of the body does not change so, the tangential acceleration is always zero over time.
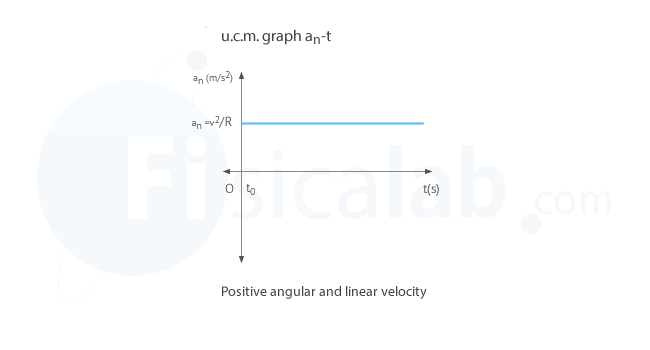
Normal acceleration – time (an–t) graph in u.c.m.
Normal acceleration in a uniform circular motion is obtained by means of the following expression:
Since the velocity is constant, the acceleration will also be constant over time.