Statement
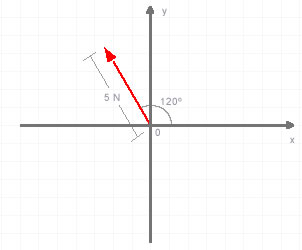
Determine the analytic expression of a force knowing that it forms an 120º angle on X – axis and it has a 5 N magnitude.
Solution
Data
- Angle with x axis α = 120º
- Magnitude of the force F = 5N
Previous considerations
Observe that exercise can be considered the complementary to this. If on the previous one we were asked to calculate the angle from the analytic expression of the force, here we are asked for the analytic expression of the force from the angle and the magnitude of the force.
On the other hand, we know that the analytic expression of a force in two dimensions is given by the general expression:
So, in this exercise we must calculate Fx and Fy.
Resolution
Ideally we should do a general idea through a graphic:
Mathematically, we can determine the expression Fx according to the definition of cosine:
For the expression Fy we will use the definition of cosine:
So, the analytic expression we are looking for is:
Observe that, instead of considering α, occassionally is better to take into account the smaller angle formed by