Statement
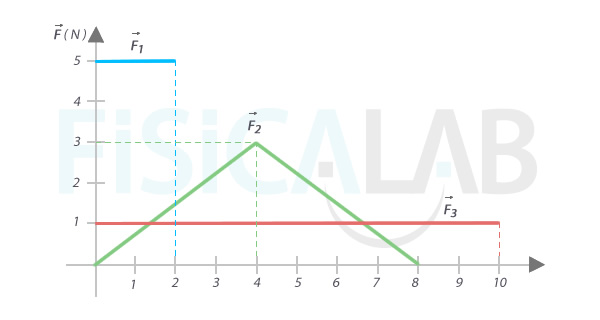
The following figure represents 3 different forces acting on 3 bodies of equal mass on identical conditions. Knowing that the 3 of them start on rest position, what of them will gain more final speed?
Solution
Data
The values of the forces over time are marked at the chart
Previous considerations
We know the impulse of a force coincides with the variation of its momentum (
Resolution
We know the area below each of the curves the forces represents coincide with the impulse numerically, so:
-
The first force´s impulse coincide with the area under the blue line, which is a rectangle. Remember the area of a rectangle is calculated multiplying the lenght by the width:
-
The impulse of the second force coincide with the are below the green lines, forming a triangle. Remember the area of the triangle is calculated by multiplying tha base by the height and then divide by two:
-
The las force´s drive coincides with the area below the red line, forming a rectangle. In this case:
So, the force number two is the responsible to produce a greater velocity over the body it acts. Watch how, despite being the first force bigger than the third one, the impulse they make while acting, therefore the final velocities the bodies gain, are the same.