¿Es función?
Enunciado
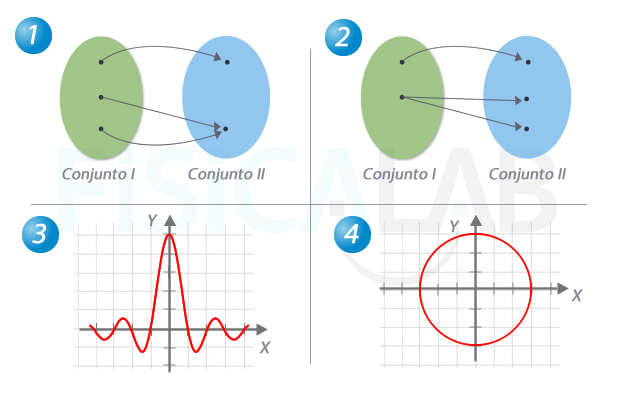
En las siguientes gráficas, determina si las relaciones entre variables podrían corresponder a lo que se conoce matemáticamente como función:
Por otro lado, haz lo mismo con las siguientes tablas:
Tabla 1
| x | 1 | 2 | 2 | 3 | 4 |
| y | 3 | 6 | 12 | 9 | 12 |
Tabla 2
| x | 0 | 0 | 1 | 2 | 0 | 2 |
| y | 0 | 1 | 0 | 0 | 2 | 1 |
| z | 0 | 1 | 1 | 2 | 2 | 3 |
Solución
Datos
Las propias ilustraciones y tablas del enunciado son todo lo que necesitamos para resolver el ejercicio.
Resolución
Sabemos que una función es una relación entre dos conjuntos en el que a cada elemento del primer conjunto le corresponde un único elemento del segundo conjunto. Dicho de otra manera: las funciones son relaciones univaludas.
A la vista de esto, podemos decir que:
- La relación de la ilustración 1 puede corresponder a una función. Vemos que a un elemento del conjunto II llegan 2 flechas, pero provienen de distintos elementos, con lo cual no deja de cumplirse la condición anteriormente señalada
- La relación de la ilustración 2 no puede corresponder a una función, ya que de un elemento del conjunto I salen dos flechas distintas, es decir, a ese valor le corresponderían dos imágenes
- La ilustración 3 podría corresponder a una función representada gráficamente. La gráfica relaciona dos conjuntos de números reales representados en el eje x y en el eje y respectivamente. Cocretamente corresponde a la función y = 5·sin(x)/x , aunque no tienes por qué saberlo. Si debes sin embargo observar que para cada valor de x sólo hay un valor de y (imagen) correspondiente
- La ilustración 4 también es una relación entre números reales, pero esta vez no es función. Corresponde a una circunferencia de radio 3. Observa que esta vez a un valor de x le pueden corresponder 2 valores de y, pues si trazas imaginariamente una recta que cruce la circunferencia verticalmente, en cualquier valor de x en el interior de la circunferencia, habrá dos valores de y asociados. (
En relación a las tablas:
-
La primera tabla no puede corresponder a una función. Aunque se trata de pares ordenados, existen dos valores de y asociados al x=2
-
La segunda tabla sí que podría corresponder a una función. Observa que, en este caso, hay 3 variables. La variable z se obtiene sumando las variables x e y. Aunque habíamos hablado de que, en una función matemática, a cada elemento de un conjunto (dominio) le correspondía un único elemento de otro (recorrido), en realidad podríamos pensar que cada pareja (x,y) forma un elemento del dominio a la que corresponde un valor z del recorrido, ya que cada pareja (x,y) de la tabla si es única. Si esto te resulta confuso, observa la siguiente tabla, que es una reorganización de la tabla 2 anterior.
(x,y) z (0,0) 0 (0,1) 1 (1,0) 1 (2,0) 2 (0,2) 2 (2,1) 3 Ahora puedes ver más claramente que a cada elemento de la columna izquierda le corresponde un único elemento de la columna derecha, independientemente de que los elementos de la columna izquierda estén formados por parejas de naturales (matemáticamente diríamos que los elementos del dominio de la función forman parte del producto cartesiano ℕxℕ ).
No hemos encontrado ninguna fórmula destacable en este ejercicio.
