Modelar situaciones reales con funciones
Enunciado
Modela las siguientes situaciones mediante funciones:
- La población de una pequeña ciudad aumenta un 15% cada año. Consideramos instante inicial el año 1983 en el que la población era de 500 habitantes. ¿Cuál será la población en el año 2050, de continuar la misma tendencia?
- La temperatura media en una comarca depende de la altura, de manera que se ha observado que se reduce 1.3 ºC por cada 160 m de ascenso . Sabiendo que el punto más bajo de la comarca está al nivel del mar, y que la temperatura media allí es de 22º, ¿qué altura habrá en su lugar más alto, a 950 m?
- El coste de una llamada al extranjero tiene un precio de conexión de 0.55 €. Durante el primer minuto el contador se mantiene estático, pero una vez transcurrido este, el coste de la llamada aumenta a razón de 0.50 € cada minuto. ¿Cuál será el coste de una llamada de 20 minutos?
- Determina una función para el cálculo del radio de cilindros tomando la altura como variable independiente y sabiendo que el volumen del mismo es siempre de 314 cm3.
- Un triángulo isósceles está inscrito en una circunferencia de radio 10 cm. Halla el área del triángulo en función de su base.
Solución
Resolución
Situación 1
Que la población aumente un 15% cada año significa, matemáticamente, que el número de habitantes de la ciudad se multiplica cada año por 1.15. Veamos:
| Año | Habiantes |
| 1983 | 500 |
| 1984 | 500·1.15=500·1.151 |
| 1985 | 500·1.15·1.15=500·1.152 |
| 1986 | 500·1.152·1.15=500·1.153 |
| 1987 | 500·1.154 |
| 1988 | 500·1.155 |
| 1989 | 500·1.156 |
De esta manera, si consideramos t la variable independiente que representa el año, h(t) será la función que obtiene el número de habitantes a partir de t. Podemos suponer que la ciudad se fundó en 1983 con 500 habitantes, de manera que el dominio será t≥1983, o más formalmente:
De esta manera,
Situación 2
Para visualizar los datos de la segunda situación y tratar de encontrar la función elaboramos la siguiente tabla:
| Altura (m) | Temperatura media (ºC) |
| 0 | 22 |
| 160 | 22-1.3 |
| 320 | 22-1.3-1.3=22-1.3·2 |
| 480 | 22-1.3·2-1.3=22-1.3·3 |
| 640 | 22-1.3·3-1.3=22-1.3·4 |
Así, parece claro que a la variable independiente altura a, en metros, le corresponde como imagen una variable dependiente que es la propia temperatura T(a). La altura mínima de la comarca es el nivel del mar (0m) y la máxima es, según se cita en el enunciado 950m. Podemos ver, a partir de los datos de la tabla, que se trata de una función lineal (lo que cambia de un año a otro es un factor de 1.3), de manera que podemos escribir:
De esta manera,
Situación 3
En este caso existen dos tramos diferenciados para la función. Resulta claro que la variable independiente es el tiempo que dura la llamada, que llamaremos t, medida en minutos. También parece claro que la variable dependiente, será el coste de la llamada, que llamaremos C(t) y que es medida en euros. La duración mínima de la llamada es de 0 minutos y no habría un máximo. Por tanto el dominio vendrá dado por:
| Duración (min) | Costo (€) |
| 1 | 0.55 |
| 2 | 0.55+0.5=0.55+0.5·1 |
| 3 | 0.55+0.5·2 |
| 4 | 0.55+0.5·3 |
| 5 | 0.55+0.5·4 |
Como puedes ver, se trata de una parte de la función que también es lineal. Para modelar los dos tramos distintos se utilizan dos ramas, cada una asociada a unos valores de t concretos. A este tipo de funciones se las denomina funciones definidas a trozos. Así:
De esta manera,
Situación 4
El volumen de un cilindro es el producto del área de la base por la altura, es decir:
Donde hemos eliminado la parte negativa de la raíz, al no poder ser un radio negativo. Por otro lado, el valor de la variable independiente h debe ser mayor o igual que cero, con lo que el dominio:
Situación 5
Recuerda, un triángulo isósceles es aquel que tiene dos lados iguales y uno desigual. Haremos un esbozo de la situación para visualizarla más claramente:
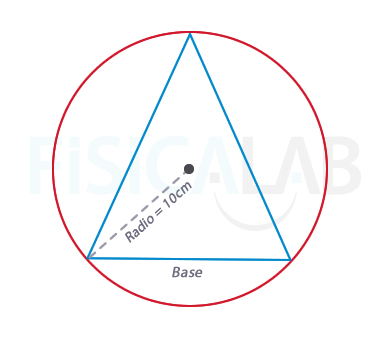
Llamaremos b a la base del triángulo, siendo la expresión de su área la mitad del producto de dicha base por la altura del triángulo: Atriángulo=b·a/2. El valor de la altura se puede poner en función del radio de la circunferencia en la cual está inscrito el triángulo. Observa la siguiente imagen:
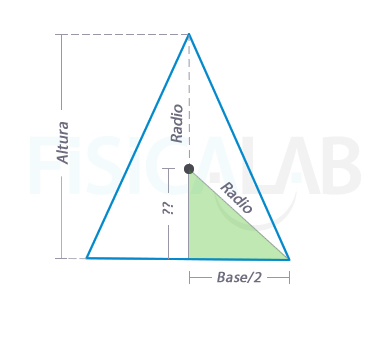
Es claro que el valor de la altura a es la suma del radio de la circunferencia, más el cateto del triángulo marcado en verde, que es un triángulo rectángulo. Podemos calcular el cateto desconocido, que llamaremos l, a través del teorema de Pitágoras, quedando:
Por tanto:
¿Es válido cualquier valor para la base? No, la raíz cuadrada no puede ser negativa, y la propia base tiene que ser mayor que cero. Dicho de otra manera, hay restricciones para el dominio según:
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
