Calcular recorrido de funciones
Enunciado
Calcula el conjunto imagen en las siguientes funciones:
Solución
Consideraciones previas
El recorrido de las funciones anteriores puede ser calculado directamente si conoces las características de las funciones básicas estudiadas en la teoría. Visita el apartado asociado si necesitas refrescar tu memoria.
Resolución
Se trata de una función constante. Su recorrido:
Función polifónica de primer grado. Su gráfica es una recta y su recorrido:
Polinomio de segundo grado que gráficamente es una parábola con las ramas hacia abajo (a<0). El recorrido de la misma comprende desde -∞ hasta la coordenada y de su máximo, situado en su vértice. Comenzamos calculando la coordenada x del vértice.
Ahora, sustituyendo esa coordenada x en la función, obtenemos la coordenada y del vértice:
Con lo que el recorrido nos queda:
Se trata de la misma función que antes pero afectada por el valor absoluto. Como sabes, el valor absoluto de un número es ese mismo número "en positivo" (si ya era positivo, el número no cambia). Para calcular el recorrido de esta función lo mejor es que representes la función sin valor absoluto gráficamente y luego se lo apliques, para ver qué pasa:
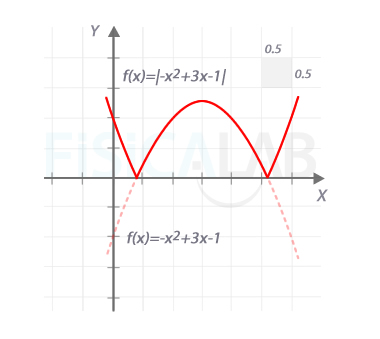
Parábola y su valor absoluto
Representación de la parábola de la función anterior, en línea roja discontinua, y su valor absoluto, en línea roja continua. Como puedes ver, en la versión de la función con valor absoluto, todo lo que antes quedaba debajo del eje x pasa a estar encima.
Por tanto, el conjunto imagen queda:
Todas las raíces de x de índice impar (13 en este caso) tienen el mismo recorrido:
La función seno siempre oscila entre -1 y 1. Como en este caso va multiplicada por tres, el recorrido nos queda:
El recorrido de la función secante es el "complementario" al de la función seno, al estar multiplicado por tres nos queda:
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
