Derivabilidad funciones por ramas y en valor absoluto
Enunciado
Averigua y explica en qué puntos no son derivables las siguientes funciones:
Solución
Consideraciones previas
Recuerda que una función es derivable en un punto cuando existe la derivada de la función en el punto. En la práctica solemos comprobar que la función f(x) sea continua en el punto, y además el valor de las derivadas laterales coincida.
En las funciones definidas a trozos los puntos de cambio de rama son problemáticos desde el punto de vista de la derivabilidad. Debemos asegurarnos que, en ellos, la función es continua y el valor de las derivadas laterales coincide.
En las funciones en valor absoluto, debemos pasarlas previamente a su forma a ramas.
Resolución
1.-
Para resolver, primero pasaremos la función a trozos. Comenzamos igualando la función en valor absoluto a 0 para conocer los puntos de cambio de rama:
En esos dos puntos, la función corta al eje X. Ahora debemos conocer el signo de la función en cada uno de los intervalos para saber en cuáles debemos cambiar el signo. En el intervalo (-∞,-2) tomaremos el -10 (por ejemplo ), en el (-2,3) tomaremos el 0 y en el (3,∞) tomaremos el 10:
Como vemos, la función en el interior del valor absoluto es negativa en el intervalo (-2,3), con lo que tendremos que cambiar su signo. Así, nos queda:
Observa que el signo "=" en el cambio de rama (es decir, los "≥" o los "≤" ) se puede poner en cualquiera de las ramas (pero solo en una para cada valor de x). Finalmente, como la función es continua, por tratarse del valor absoluto de un polinomio, estudiamos directamente las derivadas laterales en los puntos problemáticos, que son los cambios de rama:
Como las derivadas laterales son distintas no existe derivada en estos puntos, con lo que la función no es derivable en todo su dominio. Concretamente, el dominio de derivabilidad sería
2.-
Procedemos como el primer caso:
Buscamos el signo de la función encerrada en el valor absoluto en cada intervalo:
Escribimos la forma a trozos:
Como la función es continua en el punto problemático (por ser una valor absoluto), estudiamos directamente el valor de las derivadas laterales:
Podemos decir que f(x) no es derivable en x=2, siendo el dominio de continuidad
3.-
En este caso comenzamos de nuevo pasando a función a trozos, buscando los puntos de corte de la función en el interior del valor absoluto:
Buscamos el signo de la función en el interior del valor absoluto en cada intervalo:
...quedando...
Como es una función polinónica en un valor absoluto, es continua. Nos queda simplemente el cálculo de las derivadas laterales en el punto problemático (cambio de rama):
Como las derivadas laterales son distintas en ambos puntos, podemos decir que f(x) no es derivable ni en x=2 ni en x=-2, siendo el dominio de derivabilidad
Como conclusión de estos 3 primeros subapartados, podemos observar que un polinomio al que se aplica un valor absoluto es continuo, pero en general no es derivable en los puntos en los que el polinomio corta a los ejes (si los hubiera). La excepción a este comportamiento son aquellos puntos que, cortando al eje, son también puntos en los que la primera derivada del polinomio de anula (estos puntos son máximos, mínimos o puntos silla del polinomio).
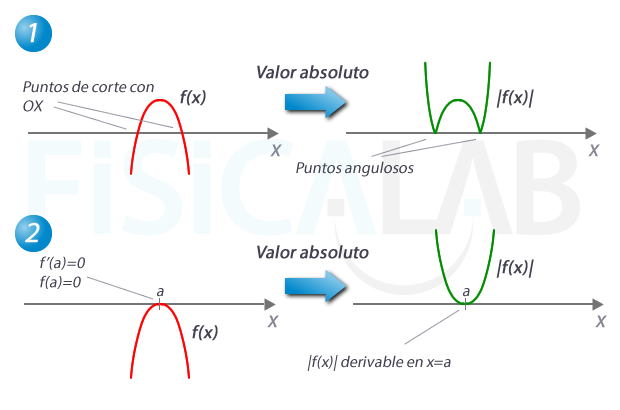
Derivabilidad de polinomios en valor absoluto
En los puntos de cortes con los ejes, si los ¡hay, el polinomio al que aplicamos el valor absoluto sigue siendo una función continua. Sin embargo, observa como, en 1, aparecen dos puntos angulosos. En 2, al estar el vértice de la parábola justamente en el corte del eje, la función en valor absoluto es, además de continua, derivable. Recuerda que el vértice de una parábola, que es su máximo o su mínimo, es justamente el lugar en el que la derivada vale 0.
4.-
Estudiamos la continuidad en el punto 0 de cambio de rama:
Como no coinciden, la función no es continua en el punto x=0 y por tanto tampoco es derivable en él. El dominio de continuidad queda
5.-
Aquí comenzamos estudiando la continuidad en el punto problemático x=-1:
En este caso, la función es continua. Ahora debemos calcular las derivadas laterales:
Por tanto, la función no es derivable en x=-1, siendo el dominio de continuidad
6.-
Resolvemos primeramente buscando la continuidad en el punto problemático x=1:
Con lo que la función es continua en x=1. Ahora vamos a buscar las derivadas laterales, para ver si coinciden:
Por tanto, la función es derivable en x=1, pudiendo decir que en este caso el dominio de continuidad coincide con el dominio de la función y es ℝ, y que:
O bien...
Observación: Puede que te estés preguntando si es posible calcular directamente las derivadas laterales sin necesidad de estudiar la continuidad para saber si una función es dericable en un punto. En realidad no. Observa la siguiente imagen:

Función a trozos no derivable
En la función de la imagen, las derivadas laterales coinciden, sin embargo la función no es derivable al no ser continua en x=a.
Intuitivamente podemos ver como la recta tangente no se mantiene constante, ni varía de manera "suave" al aproximarnos al punto x=a, como exigiría la derivabilidad. Por el contrario, presenta un salto. Y esto a pesar de coincidir la pendiente en ambos laterales de x=a, pues f'(a-)=f'(a+).
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
