Movimiento en Media Luna
Enunciado
Un cuerpo se desplaza entre dos instantes cualesquiera de tiempo siguiente una trayectoria circular de radio 5 metros tal y como puedes ver en la figura.
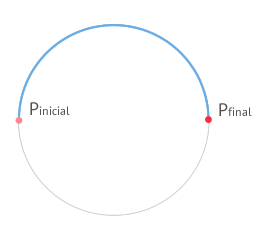
Determina:
- El vector desplazamiento del cuerpo y el espacio recorrido suponiendo el origen del sistema de referencia situado en el punto de inicio del movimiento
- El vector desplazamiento del cuerpo y el espacio recorrido suponiendo el origen del sistema de referencia situado en el centro del semicírculo
Solución
1. Nos encontramos en una situación como la de la figura siguiente

El vector desplazamiento corresponde al vector que une el punto inicial con el final. Observando el dibujo podemos ver que el vector tendrá un módulo igual al diámetro de la semicircunferencia, su dirección será la del eje x y su sentido positivo.
Podríamos haberlo calculado analíticamente, a partir de la expresión del vector desplazamiento considerando
En cuanto al espacio recorrido, dado que la trayectoria del movimiento es una semicircunferencia, su valor coincide con la longitud de dicha semicircunferencia:
2. Nos encontramos en una situación como la de la figura siguiente
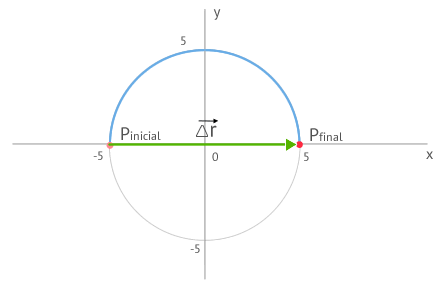
El vector desplazamiento corresponde al vector que une el punto inicial con el final. En este caso
Como puedes ver, el vector desplazamiento tiene el mismo valor que en el punto 1, a pesar de haber elegido un origen para el sistema de referencia distinto. El desplazamiento del cuerpo es por tanto independiente de donde sitúes el origen.
En relación al espacio recorrido, los cálculos son los mismos que en el apartado anterior.
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
