Statement
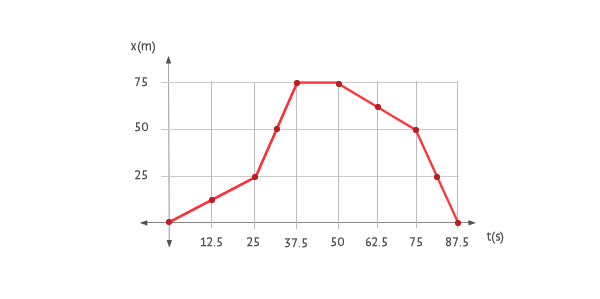
The following graph of position-time ( x-t ) corresponds to a body moving in a straight trajectory. Determine the equation of motion for each segment and its velocity-time graph. From the expression for each segment, search for a general expression in the form of a function defined by segments, called a piecewise-defined function, for the position and one for the velocity.
Solution
Data
- The data of the problem are implicit in the graph
Preliminary considerations
- The general expression of uniform linear motion is given by
-
The term accompanying t corresponds to the velocity of the body according to the general expression. Don't forget that the instantaneous velocity of a body is defined as the derivative of the position with respect to time, so:
therefore, the velocity is the slope of each straight line in the graph position-time ( x-t )
- Remember that the position, velocity and acceleration are vector quantities. In the event that the trajectory is a straight line, we can use the sign convention in rectilinear motion and use scalars (numbers) instead of vectors
Resolution
There are 5 segments, each one with its own expression for its u.r.m.
Segment I ( 0 < t < 25 )
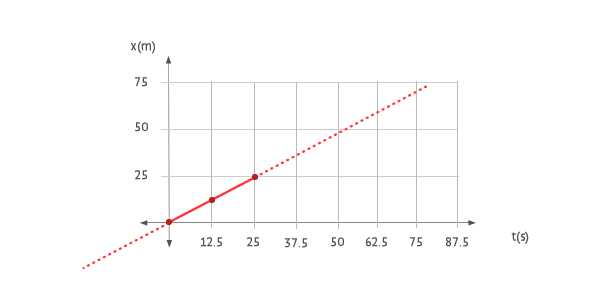
The equation of motion in this segment is:
Segment II ( 25 < t < 37.5 )
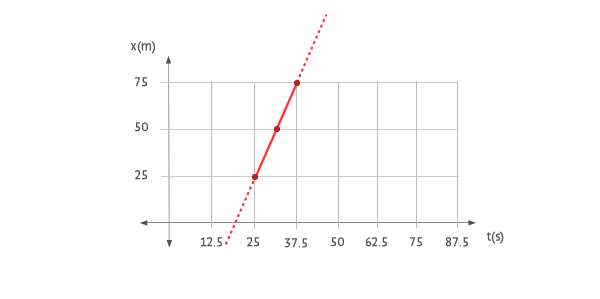
Now, to determine x02 we can use the value of the straight line at any instant of time, e.g. t = 37.5 s, obtaining:
The equation of motion in this second segment:
Segment III ( 37.5 < t < 50 )
The body is stationary in this section, since there is no variation of x(t) over time. This means that:
The equation of motion for the third segment:
Segment IV ( 50 < t < 75 )
The slope (velocity) on this segment is equal to the slope of the first segment but in the opposite direction. Following the sign convention for rectilinear motion from above, this means that the motion has changed its direction and is directed to the starting point. Let's see:
Now, to determine x04 we can use the value of the straight line at any time, e.g. t = 50 s, resulting in:
For the fourth segment, we have the equation of motion:
Segment V ( 75 < t < 87.5 )
Again, the slope in this segment (velocity) is like in the second segment but in opposite direction. Following the sign convention for rectilinear motion from above, this means that the motion has changed its direction and is directed to the starting point. Let's see:
We calculate the initial position using as reference the final point on the graph:
Finally, for the 5th segment the equation of motion is:
Once obtained the expression for each section, we can write a single expression in the form of a piecewise-defined function:
And for the velocity...

