Ayúdanos a mantenernos en órbita
¿Nuestros contenidos te están resultando de utilidad?
Con un pequeño gesto podremos mantenernos en órbita. Regístrate para acceder a contenidos y funcionalidad exclusiva. Además, con tu ayuda podremos continuar ofreciendo nuestros servicios de manera gratuita para miles de estudiantes en todo el mundo. Te ofrecemos:
- Un campus virtual orientado a la gamificación
- Nuevos contenidos premium
- Nuevas simulaciones
- Acceso prioritario a nuestro plantel de profesores de física y matemáticas
Statement
Solution
Data
v = 5 km / h = 5000 m / 60 min / h = 83.33 m / min -- Velocity
x0 = 0 m -- Initial position.
t0 = 0 min -- Start time
tf = 15 min -- Final time
Resolution
Since the person walks in a straight line and with constant velocity, we have a uniform rectilinear motion. The position equation for this type of motion is x = x0 + v · t . This way, by applying the formula for the position we can calculate its position, for examples, at four different times like t = 0, 5, 10 and 15 minutes
| t | x |
|---|---|
| 0 | x = 0 + 83.33 · 0 = 0 |
| 5 | x = 0 + 83.33 · 5 = 416.65 |
| 10 | x = 0 + 83.33 · 10 = 833.3 |
| 15 | x = 0 + 83.33 · 15 = 1249.95 |
To solve the exercise, and for simplicity, you can observe that we have taken meters as unit of position and minutes as unit of time. Then we represent pairs of values obtained from points in a graph where position is given by the x-axis and time by the t-axis.
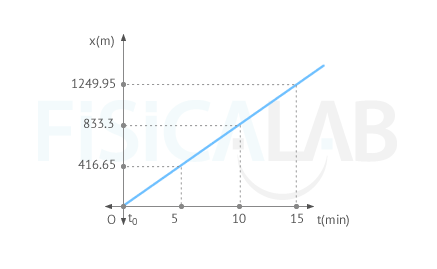
Notice that we used 4 points to draw the graph although it is enough with only two of them, since a u.r.m. graph is a straight line and a line can be drawn knowing only two of its points.