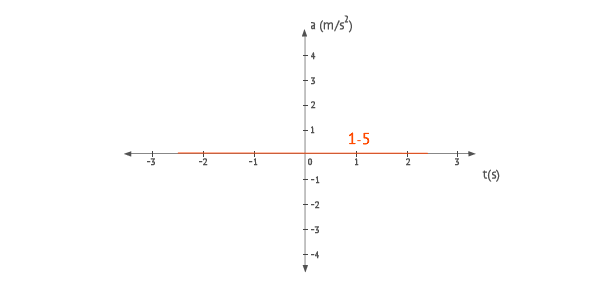Draw graphs from u.r.m. equations

Preliminary considerations

• We can identify each of the previous expressions with the uniform rectilinear motion general expression $x=x_0+v\cdot t$
• The independent term corresponds to the initial position x₀

• The term accompanying t corresponds to the velocity of the body according to the general expression. Don't forget that the instantaneous velocity of a body is defined as the derivative of the position with respect to time, therefore:

  $$v=\frac{dx}{dt}$$

• Remember that in any uniform rectilinear motion the acceleration is zero. The instantaneous acceleration is defined as the derivative of the velocity with respect to the time. Since the velocity is constant, the derivative of a constant is zero. For example, to the first movement:

  $$a=\frac{dv}{dt}=\frac{d}{dt}\left(\frac{dx}{dt}\right)=\frac{d}{dt}\frac{d}{dt}(3+4·t)=\frac{d}{dt}\left(4\right)=0 m/s^2$$ 

• Remember that the position, velocity and acceleration are vector quantities. In the event that the trajectory is a straight line, we can use the sign convention in rectilinear motion and use scalars (numbers) instead of vectors

• Equation 5 is not written in the general form of the u.r.m., so we have to modify it: we move factor that accompanies the x to the right side getting:

  $$3·x=9+12·t\Rightarrow x=\frac{1}{3}·(9+12·t)\Rightarrow x=3+4·t$$

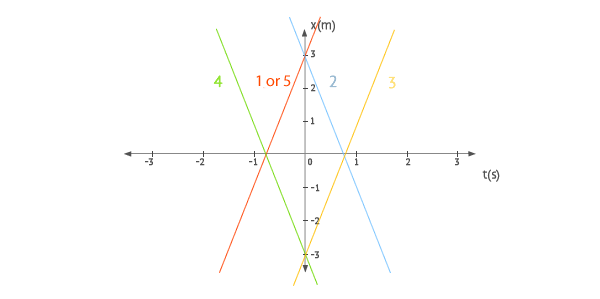
  Observe that we now have an expression equal to the first motion. Therefore, its graph will also be the same

Resolution

Position graphs

To determine the position graph in each motion, we just give a couple of values to t, get the corresponding x values and draw the straight line. We get:

Velocity graphs

The velocity is constant in all motions so the corresponding graphs are horizontal straight lines:

Acceleration graphs

The acceleration graphs of all the motions are the same.