Razones Trigonométricas de Ángulos Complementarios
Se dice que dos ángulos α y β son ángulos complementarios cuando su suma es 90º (α + β = 90º ) o lo que es lo mismo π/2 rad ( α + β = π/2 rad )
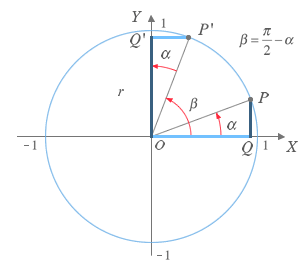
Ángulos Complementarios
Si el segmento OP de la figura forma un ángulo α con el semieje positivo complementario con un ángulo β determinado por el segmento OP' se cumple que α+β es 90º (π/2 rad), esto implica que β = π/2 - α.
Si observas la figura en la que se representan dos ángulos complementarios α y β, el triángulo OQP es equivalente al triángulo OQ'P' ya que poseen la hipotenusa y dos ángulos (α) iguales. QP = Q'P' y OQ= OQ'
Por tanto:
| Razones | Razones inversas |
|---|---|
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
Navegación
Loading...
