Razones Trigonométricas de Cualquier Ángulo

Una vez definidas las razones trigonométricas de ángulos agudos (<90º), a partir de un triángulo rectángulo, podemos extender su definición para ángulos de cualquier amplitud. En este capítulo vamos a estudiar:

Razones trigonométricas en la circunferencia goniométrica
Propiedades de las razones trigonométricas
Sus signos según el cuadrante del ángulo
Cómo calcular el ángulo conocida una de sus razones
- Método gráfico
- Calculadora

¿Vamos a ello?

Razones trigonométricas en la circunferencia goniométrica

Para determinar las razones trigonométricas de cualquier tipo de ángulo utilizaremos una circunferencia goniométrica.

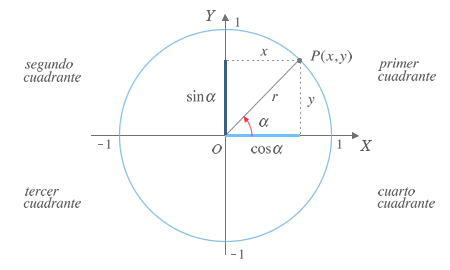
Circunferencia goniométrica

Circunferencia cuyo radio es 1 (la unidad) y se encuentra centrada en el origen de un sistema de coordenadas. A cada uno de sus puntos P(x,y) le corresponde un único ángulo α definido entre el semieje positivo de abcisas (eje x) y el segmento OP. Su intersección con los ejes de coordenadas la divide en cuatro partes denominadas cuadrantes.

La utilización de una circunferencia goniométrica no es casual, ya que nos simplifica la visualización de las razones, dado que el radio es la unidad:

$\sin α = \frac{y}{r} = \frac{y}{1} = y \cos α = \frac{x}{r} = \frac{x}{1} = x$

Por tanto, las razones trigonométricas de cualquier ángulo se definen en función de las proyecciones sobre los ejes x e y:

Razones	Razones inversas
$\sin α = y$	$csc α = \frac{1}{y}$
$\cos α = x$	$sec α = \frac{1}{x}$
$tg α = \frac{y}{x}$	$cotg α = \frac{x}{y}$

Puedes usar una calculadora para obtener el valor de la razón de un ángulo cualquiera.Introduce el ángulo deseado, en grados o radianes (según tengas configurada tu calculadora en Deg - grados sexagesimales ó Rad - radianes), y pulsa la tecla correspondiente tecla seno calculadora , tecla coseno calculadora ó tecla tangente calculadora .

Experimenta y Aprende

Definición de razones trigonométricas

La figura muestra una circunferencia goniométrica y un punto P cualquiera de ella. Observa que a cada punto le corresponde un ángulo α formado entre el segmento OP y el semieje X positivo. Puedes cambiar el valor de α arrastrando el deslizador inferior. Comprueba que el sin α coincide con el valor de la coordenada y y el cos α con el valor de la coordenada x del punto P.

De una manera más gráfica, el cos α corresponde con la longitud de la proyección del punto sobre el eje x y el sin α sobre el eje y. Adicionalmente tg α corresponde con la proyección sobre la recta tangente en el punto (1,0). ¿Sabrías decir por qué? En cualquier caso, estas longitudes se consideran positivas si las proyecciones se encuentran sobre los semiejes positivos y negativas si se encuentran sobre los semiejes negativos.

Por otro lado, puedes pulsar el botón Inversas para visualizar la representación en la circunferencia de las razones trigonométricas inversas. La cotg α, inversa de la tg α, se obtiene como el corte entre la recta tangente a la circunferencia goniométrica en (0,1) y la recta que contiene a los puntos O y P. La csc α, inversa del sin α, se obtiene uniendo la cotangente con el origen. Finalmente, la sec α, inversa del cos α, se obtiene uniendo la tangente con el origen.

Las razones de ángulos mayores de 360º (2π rad) o ángulos negativos son iguales a las de sus ángulos equivalentes en el primer giro. Así, por ejemplo:

sin(750º)=sin(30º)=0.5
sin(-π/2)=sin(3π/2)=-1

Propiedades de las razones trigonométricas de cualquier ángulo α

Dado que el seno y el coseno de cualquier ángulo α corresponden respectivamente con los valores y y x de la circunferencia goniométrica, sólo pueden tomar valores entre -1 y 1:

$\begin{matrix} - 1 \leq \sin α & \leq 1 \end{matrix}; \begin{matrix} - 1 \leq \cos α & \leq 1 \end{matrix}$

Además, si aplicamos el teorema de Pitágoras se cumple que:

$x^{2} + y^{2} = 1^{2}$

Sustituyendo x e y obtenemos lo que se conoce como la identidad fundamental de la trigonometría, que ya habíamos demostrado cuando estudiamos las razones de los ángulos agudos:

$\sin^{2} α + \cos^{2} α = 1$

Signos de las razones trigonométricas por cuadrantes

Signos de las razones trigonométricas según cada cuadrante

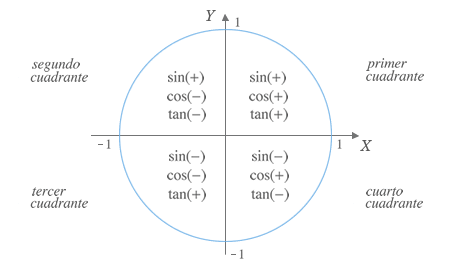
Así pues, los valores del seno y del coseno (de los que se derivan los del resto de razones) para los ángulos de 0º (ó 0 rad), 90º (ó π/2 rad), 180º (ó π rad), 270º (ó 3π/2 rad) corresponden con los valores que tengan las coordenadas de los puntos de intersección de la circunferencia goniométrica con los ejes. Finalmente, recuerda que las razones de 360º (2π rad) son iguales a las de 0º (0 rad).

α	0º	90º	180º	270º
sen	$0$	$1$	$0$	$- 1$
cos	$1$	$0$	$- 1$	$0$
tg	$0$	$\infty$	$0$	$- \infty$
cosec	$\infty$	$1$	$\infty$	$- 1$
sec	$1$	$\infty$	$- 1$	$\infty$
cotg	$\infty$	$0$	$\infty$	$0$

Ejemplo

a) Calcular las razones trigonométricas de un ángulo α situado en el segundo cuadrante y cuyo cos α = -0.57

b) Repite el ejercicio suponiendo ahora que α está situado en el tercer cuadrante

Ver solución

Cálculo de un ángulo a partir de las razones

Hasta ahora hemos hablado de como calcular, a partir de un ángulo concreto, el seno, el coseno o cualquier otra razón. Se puede hacer también el camino inverso, es decir, se puede obtener un ángulo a partir del valor de su razón. Estudiaremos un método gráfico y también mediante la calculadora.

Método gráfico

En primer lugar tenemos que fijarnos si conocemos el valor del seno, del coseno o de la tangente del ángulo.

Si conocemos el seno
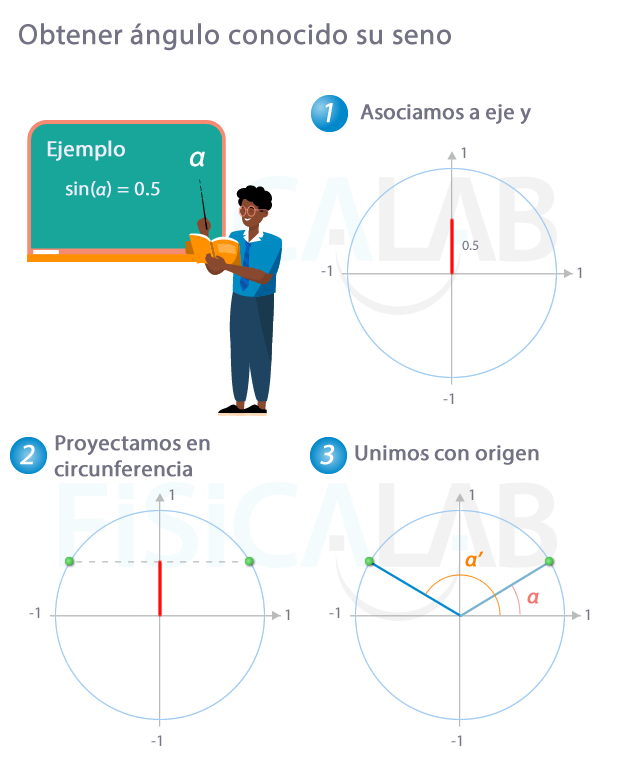
Calcular el ángulo conocido el seno
Proceso para obtener el ángulo a partir de su seno.
1. En primer lugar tomamos la porción del semieje y que corresponda, según el valor del seno. En este caso, tomamos 0.5 (medio semieje)
2. Proyectamos dicha distancia sobre la circunferencia, trazando una línea paralela al eje x. Señalamos los puntos de corte (en verde)
3. Finalmente unimos los dos puntos de corte obtenidos en el paso 2 con el origen. Los dos ángulos así obtenidos tienen el mismo valor de seno. Es decir sin(α)=sin(α') =0.5 Puedes usar un transportador de ángulos para medir dichos ángulos.
Si conocemos el coseno
Calcular el ángulo conocido el coseno
Proceso para obtener el ángulo a partir de su coseno.
1. En primer lugar tomamos la porción del semieje x que corresponda, según el valor del coseno. En este caso, tomamos -0.5 (medio semieje)
2. Proyectamos dicha distancia sobre la circunferencia, trazando una línea paralela al eje y. Señalamos los puntos de corte (en verde)
3. Finalmente unimos los dos puntos de corte obtenidos en el paso 2 con el origen. Los dos ángulos así obtenidos tienen el mismo valor de coseno. Es decir cos(α)=cos(α')=-0.5 Puedes usar un transportador de ángulos para medir dichos ángulos.
Si conocemos la tangente
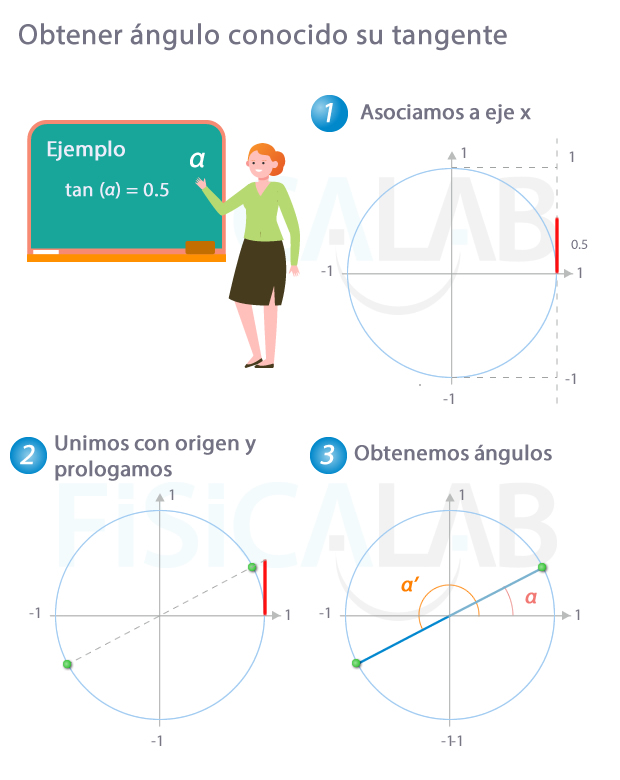
Calcular el ángulo conocida la tangente
Proceso para obtener el ángulo a partir de su tangente.
1. En primer lugar tomamos la recta perpendicular al eje x y tangente a la circunferencia en el punto (0,1) y sobre ella tomamos el valor de la tangente. Ten presente que esta recta puede ser mayor que 1, o menor que -1, ya que -∞<tan(α)<∞. En este caso, tomamos 0.5 unidades de dicha recta.
2. Unimos con el origen de coordenadas y prolongamos, buscando los 2 cortes con la circunferencia (señalados por los puntos verdes)
3. Finalmente obtenemos los 2 ángulos posibles. Estos tienen el mismo valor de tangente, es decir tan(α)=tan(α')=0.5 Puedes usar un transportador de ángulos para medir dichos ángulos.
Si conocemos alguna razón inversa

Si conocemos el valor de la cosecante (cosec(α)), la secante (sec(α)) o la cotangente (cotan(α)), simplemente hacemos su valor inverso sin(α)=1/cosec(α), cos(α)=1/sec(α) ó tan(α)=1/cotan(α), y obtenemos los posibles valores de α con el procedimiento ya indicado anterioriormente.

Calculadora

Al igual que es posible utilizar la calculadora para determinar el seno, el coseno o la tangente de un ángulo, es posible también hacer el camino inverso, es decir, conocido el valor del seno, el coseno o la tangente determinar α. Para ello la calculadora cuenta con las funciones arcoseno, arcocoseno y arcotangente. Puedes "leer" estas funciones como "arco cuyo seno vale...", "arco cuyo coseno vale..." y "arco cuya tangnte vale..." respectivamente.

Para determinar con la calculadora el ángulo cuyo seno, coseno o tangente conoces, introduce en primer lugar en la calculadora el valor de la razón conocida. Posteriormente pulsa la tecla shift (segunda función) y pulsa la tecla tecla seno calculadora , tecla coseno calculadora ó tecla tangente calculadora , según la razón que conozcas. El valor devuelto será el ángulo en grados sexagesimales, grados centesimales o radianes, según tengas configurada tu calculadora.

Convenio de cuadrantes en calculadora para obtener ángulo según razón

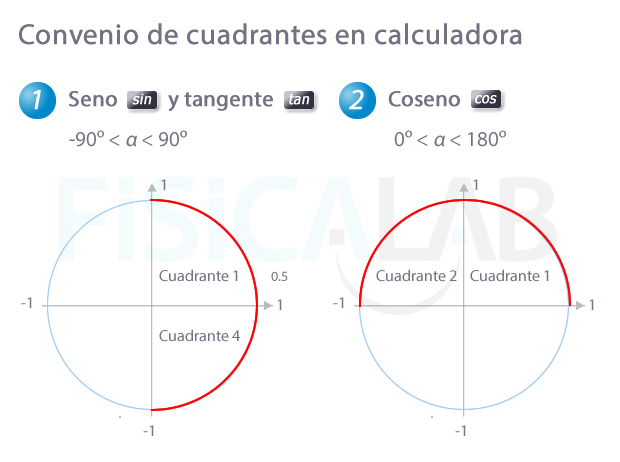
Rango de ángulos devueltos por calculadora según razón

El valor del ángulo devuelto por la calculadora al aplicar el arcoseno o el arcotangente está entre el primer y el cuarto cuadrante (expresado como un ángulo negativo). En el caso del arcocoseno, el valor del ángulo devuelto se encuentra entre el primer y el segundo cuadrante.

A partir de ahí, y recordando que existen dos ángulos en el primer giro de la circunferencia goniométrica que tienen la misma razón ¿qué ocurre si quieres obtener el otro? Puedes ayudarte de la siguiente tabla.

	Seno	Coseno	Tangente
Cuadrantes con la misma razón	El seno de un ángulo en el primer cuadrante coincide con el seno en el segundo. El seno de un ángulo en el cuarto cuadrante coincide con el seno en el tercero.	El coseno de un ángulo en el primer cuadrante coincide con el coseno en el cuarto. El coseno de un ángulo en el segundo cuadrante coincide con el coseno en el tercero.	La tangente de un ángulo en el primer cuadrante coincide con la tangente en el tercero. La tangente de un ángulo en el cuarto cuadrante coincide con la tangente en el segundo.
Calculo a realizar	(Grados sexagesimales)180º-α (Radianes)π-α	-α	(Grados sexagesimales)180º+α (Radianes)π+α
Propiedad en la que nos basamos	(Grados sexagesimales)sin(180-α)=sin(α) (Radianes)sin(π-α)=sin(α)	cos(-α)=cos(α)	(Grados sexagesimales)tan(180+α)=tan(α) (Radianes)tan(π+α)=tan(α)

Seno

Coseno

Tangente

Cuadrantes con la misma razón

El seno de un ángulo en el primer cuadrante coincide con el seno en el segundo.

El seno de un ángulo en el cuarto cuadrante coincide con el seno en el tercero.

El coseno de un ángulo en el primer cuadrante coincide con el coseno en el cuarto.

El coseno de un ángulo en el segundo cuadrante coincide con el coseno en el tercero.

La tangente de un ángulo en el primer cuadrante coincide con la tangente en el tercero.

La tangente de un ángulo en el cuarto cuadrante coincide con la tangente en el segundo.

Calculo a realizar

(Grados sexagesimales)180º-α

(Radianes)π-α

-α

(Grados sexagesimales)180º+α

(Radianes)π+α

Propiedad en la que nos basamos

(Grados sexagesimales)sin(180-α)=sin(α)

(Radianes)sin(π-α)=sin(α)

cos(-α)=cos(α)

(Grados sexagesimales)tan(180+α)=tan(α)

(Radianes)tan(π+α)=tan(α)

Una cuestión de notación: En la mayoría de las calculadores, verás escrito sobre las teclas tecla seno calculadora , tecla coseno calculadora ó tecla tangente calculadora las palabras sin^-1, cos^-1 y tan^-1. Se trata en realidad de las funciones arcoseno, arcocoseno y arcotangente respectivamente. El ^-1 del exponente indica función inversa (del seno, coseno o de la tangente).

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José L. Fernández es ingeniero de telecomunicaciones, profesor y curioso por naturaleza. Dedica su tiempo libre a escribir artículos para Fisicalab y a ayudar a Link a salvar Hyrule.

Apartados relacionados

El apartado no se encuentra disponible en otros niveles educativos.