Ecuación trigonométrica con resultado en grados sexagesimales

De igual forma que en el ejemplo anterior y tal y como estudiamos en el apartado de razones trigonométricas de los ángulos de 30º, sabemos que $\cos \left(30\right) =\raisebox{1ex}{$\sqrt{3}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$. Por tanto, ya tenemos que una de las soluciones se obtiene por medio de la siguiente ecuación x + 15º = 30º. De aquí, x = 30º-15º = 15º.

Por otro lado, si recordamos el apartado de ángulos opuestos, existe otro ángulo situado en el cuarto cuadrante que posee el mismo valor que cos 30º.

Ángulos Opuestos

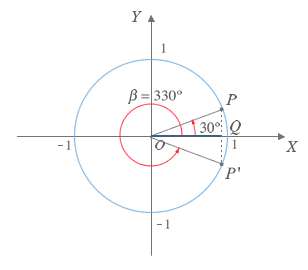
Si dibujamos un ángulo de 30º sobre la circunferencia goniométrica, su coseno es el valor de la coordenada x del punto P (gráficamente la longitud del segmento azul OQ). Observa que podemos obtener ese mismo valor de coseno con otro ángulo β = 360º-30º = 330º situado en el cuarto cuadrante. De hecho siempre se cumple que para cualquier ángulo α

$$\begin{gathered} \cos \alpha = \cos \left(360º-\alpha \right) \\ \cos \alpha = \cos \left(2\pi -\alpha \right) \end{gathered}$$

De esta forma también se cumple que x + 15º = 330º, y de aquí x = 315º. Por tanto:

$$x=\left\{\begin{array}{l}15º+360º·k\\ 315º+360º·k\end{array}\right. k\in \mathrm{\mathbb{Z}}$$