Modelado de situaciones reales con funciones a trozos

Resolución

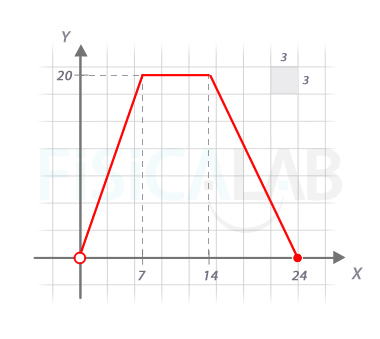
Situación 1

En la primera situación debemos encontrar una función que nos dé la dosis del fármaco en función del día en que nos encontramos. La variable independiente representa, por tanto, el tiempo, medido en días. Así, se trata de 3 tramos. Veamos.

El primero estará definido para la primera semana, es decir, 0<x<7. En él, partimos de una cantidad mínima de 6 mg, y sumamos 2mg al día, es decir y=6+2x.

El segundo se inicia en la segunda semana, es decir, el día 7 y termina una semana después, es decir 7<x<14. En este intervalo la dosis es constante, e igual al valor alcanzado en el día 7, es decir 6+2·7=20. Con lo que y=20.

Finalmente la tercera rama abarca desde el día 14 hasta el 24 (14+10), con lo que 14<x<24. En ella la disminución de la dosis es lineal. Comienza en 20 mg y debe concluir en 0. Como no es trivial como las anteriores, recurriremos a la expresión explícita de una recta y=a·x+b. Sabemos que cuando x=14, y=20, y que cuando x=24, y=0, con lo que podemos resolver el siguiente sistema:

$$\begin{gathered} y=a·x+b\Rightarrow \left\{\begin{array}{l}20=14·a+b\\ 0=24a+b\end{array}\right.\left\{\begin{array}{l}-20=-14·a-b\\ 0=24a+b\end{array}\right.\Rightarrow -20=10a\Rightarrow a=-2\Rightarrow \\ \Rightarrow b=48\Rightarrow \boxed{y=48-2x} \end{gathered}$$

Finalmente, colocando los signos igual (≤) en los extremos de los intervalos, nos queda la función por ramas:

Modelado primera situación

$$f\left(x\right)=\left\{\begin{array}{ccc}6+2x& \text{si}& 0<x<7\\ 20& \text{si}& 7\le x<14\\ 48-2x& \text{si}& 14\le x\le 24\end{array}\right.$$

Dom_f=(0,24] ; Rec_f=[0,20]

Ten presente que los signos igual ( en este caso ≤ ) podrían ir en otras ramas a las elegidas, pero hemos considerado que no tiene sentido definir la función para días negativos (tampoco justo para el día 0), y que como máximo la dosis está reglada hasta el día 24 (incluido).

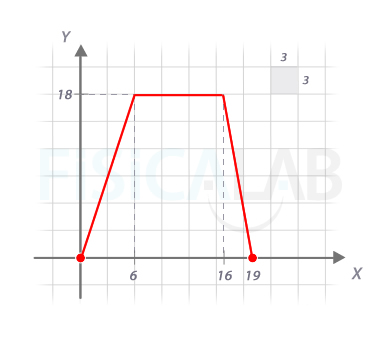
Situación 2

En el segundo caso debemos encontrar una función que nos dé la velocidad del móvil en función del tiempo. La variable independiente x representa, por tanto, el tiempo, medido en segundos y la variable dependiente y=f(x), la velocidad medida en m/s. Así, se trata de 3 tramos. Veamos.

El primer tramo es un m.r.u.a.. Para definir el intervalo para el cual está definido debemos conocer el tiempo que tarda en alcanzar los 18m/s. Podemos aplicar la ecuación del m.r.u.a. v=v₀+a·t y despejar el tiempo o bien saber que el cuerpo aumenta su velocidad 3m/s cada segundo, con lo que t=18/3=6s. En resumen 0<x<6 (recuerda que hemos llamado x al tiempo). En este tramo y=3·x.

En el segundo tramo, la velocidad permanece constante 10 segundos. Esto es, 6<x<16. En este tramo y=18.

Finalmente en la tercera rama tenemos de nuevo un m.r.u.a. El móvil permanece en este tramo t=3s, con lo que 16<x<19. Para hallar la expresión concreta correspondiente al tramo, hay que considerar que la velocidad varía de manera lineal ( y=a·x+b ), que en x=16, y=18 y que en x=19, y=0, con lo que resolviendo el sistema nos queda:

$$\begin{gathered} \begin{array}{c}18=a·16+b\\ 0=a·19+b\end{array}\Rightarrow \begin{array}{c}-18=-a·16-b\\ 0=a·19+b\\ -18=3·a \\ \Rightarrow \boxed{a=-6} \end{array}\Rightarrow \boxed{b=114} \end{gathered}$$

Es decir, y=114-6·x. Otra forma de proceder es aplicar la ecuación de la velocidad en el m.r.u.a, v=v₀+a·t, con a=-6m/s², pero "centrándola" en x=16, en lugar de en x=0, con lo que nos queda: y=18-6·(x-16). Si necesitas ampliar información sobre este último procedimiento visita el apartado de transformación de funciones, concretamente el apartado sobre desplazamientos horizontales.

En definitiva, la función por ramas, colocando los signos igual (≤) queda:

Modelado segunda situación

$$f\left(x\right)=\left\{\begin{array}{ccc}3·x& \text{si}& 0\le x\le 6\\ 18& \text{si}& 6<x<16\\ 18-6·\left(x-16\right)& \text{si}& 16\le x\le 19\end{array}\right.$$

Dom_f=[0, 19] ; Rec_f=[0, 18]

De nuevo, ten presente que los signos igual ( ≤ ) podrían ir en otras ramas a las elegidas.

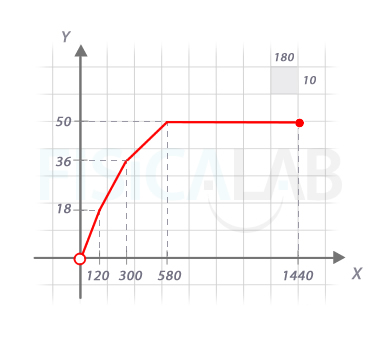
Situación 3

En primer lugar obtenemos una función que nos dé el precio de aparcar (variable dependiente y=f(x) ) en función de los minutos que pasa el coche en el parking (variable independiente x) . Así, se trata de 4 tramos lineales. Veamos.

El primer tramo es inmediato: y=0.15·x y corresponde a 0≤x≤120.

Para el segundo tramo hemos de tener en cuenta que comenzaremos pagando todo el primer tramo (0.15·120=18), y después sumaremos 0.1$ por cada minuto extra, es decir, y=18+0.1·(x-120). Este tramo "dura" 3 horas=180 minutos, esto es, 120<x<300.

El tercer tramo, siguiendo un razonamiento similar, sigue la forma y=36+0.05·(x-300). Para saber cuánto dura el tramo debemos ver cuando se alcanzan los 50$ de máximo.

$$50=36+0.05·\left(x-300\right)\Rightarrow \frac{14}{0.05}+300=x\Rightarrow x=580$$

Con lo que para el tercer tramo se cumple 300<x<580.

Finalmente, el cuarto tramo dura hasta que acaba el día, que tiene 24 horas = 1440 minutos, 580<x<1440. En él, y=50. A continuación tienes la función a trozos y su representación. Observa que, como hasta ahora, hemos colocado los signos igual ( ≤ ) de los límites de las ramas en cualquiera de las 2 posibles para cada límite, pero solo en una de ellas:

Modelado tercera situación

$$f\left(x\right)=\left\{\begin{array}{ccc}0.15·x& \text{si}& 0<x\le 120\\ 18+0.1·\left(x-120\right)& \text{si}& 120<x\le 300\\ 36+0.05·\left(x-300\right)& \text{si}& 300<x\le 580\\ 50& \text{si}& 580<x\le 1440\end{array}\right.$$

Dom_f=(0, 1440] ; Rec_f=(0, 50]

Ahora, si te sientes un verdadero geek de las matemáticas, observa como puedes "extender" la función para que nos devuelva el precio del parking, independientemente del número de días considerado. Por un lado, tendrás que sumar en cada rama el número de días ya concluidos, con un precio de 50 euros cada día completo. Esto es, el cociente de la división del número de minutos x entre 1440. El cociente debe ser un número entero, y se obtiene a partir de la prueba de la división. Esta nos dice que el dividendo D es igual al cociente C por el divisor d más el resto o residuo R, con lo que:

$$D=C·d+R\Rightarrow C=\frac{D-R}{d}$$

El dividendo D es precisamente x, el divisor d es 1440, pero debemos expresar el resto en función de estos valores. Podemos hacerlo con la notación x mod 1440 que significa justamente "el resto de dividir x entre 1440".

Por otro lado, allá donde antes ponía x ahora debemos poner ese resto, es decir, x mod 1440. En resumidas cuentas, la función final es:

$$f\left(x\right)=\left\{\begin{array}{ccc}50·\frac{x-\left(x mod 1440\right)}{1440}+0.15·\left(x mod 1440\right)& \text{si}& 0\le \left(x mod 1440\right)\le 120\\ 50·\frac{x-\left(x mod 1440\right)}{1440}+0.1·\left(\left(x mod 1440\right)-120\right)& \text{si}& 120<\left(x mod 1440\right)\le 300\\ 50·\frac{x-\left(x mod 1440\right)}{1440}+36+0.05·\left(\left(x mod 1440\right)-300\right)& \text{si}& 300<\left(x mod 1440\right)\le 580\\ 50·\frac{x-\left(x mod 1440\right)}{1440}+50& \text{si}& 580<\left(x mod 1440\right)<1440\end{array}\right.$$

Esta vez el dominio es Dom_f=(0,∞) y el recorrido Rec_f=(0,∞).