Análisis gráfica movimiento rectilíneo uniforme
Enunciado
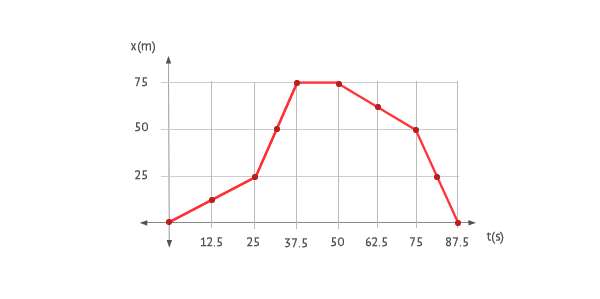
La siguiente gráfica de posición - tiempo ( x-t ) corresponde a un cuerpo que se mueve con trayectoria recta. Determina la ecuación del movimiento en cada tramo y su gráfica de velocidad - tiempo. A partir de la expresión para cada tramo, busca una expresión general en forma de función definida a trozos para la posición y otra para la velocidad.
Solución
Datos
- Los datos del problema están implícitos en la propia gráfica
Consideraciones previas
- La expresión general del movimiento rectilíneo uniforme viene dada por
-
El término que acompaña a t corresponde con la velocidad del cuerpo según la expresión general. No olvides que la velocidad instantánea de un cuerpo se define como la derivada respecto al tiempo de la posición, por tanto:
La velocidad es por tanto la pendiente de cada recta en la gráfica posición - tiempo ( x-t )
- Recuerda que la posición, la velocidad y la aceleración son magnitudes vectoriales. En el caso de que la trayectoria sea una recta, podemos usar el convenio de signos en movimientos rectilíneos habitual para usar escalares (números) en lugar de vectores
Resolución
Existen 5 tramos, cada uno de los cuales tiene su propia expresión del m.r.u.
Tramo I ( 0 < t < 25 )
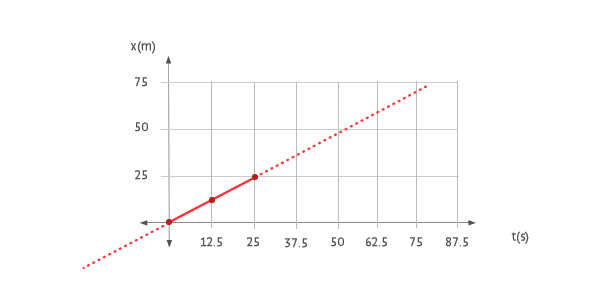
La ecuación del movimiento en este tramo:
Tramo II ( 25 < t < 37.5 )
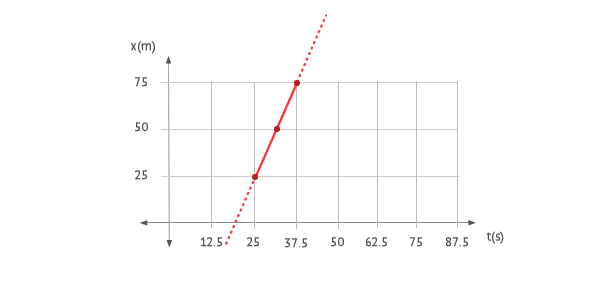
Ahora, para determinar x02 podemos usar el valor de la recta en cualquier instante de tiempo, por ejemplo t = 37.5 s, quedando
La ecuación del movimiento en este segundo tramo:
Tramo III ( 37.5 < t < 50 )
El móvil permanece quieto en este tramo, ya que a lo largo del tiempo x(t) no varía. Esto quiere decir que:
La ecuación del movimiento para el tercer tramo:
Tramo IV ( 50 < t < 75 )
La pendiente ( velocidad ) en este tramo es igual a la del primero pero de sentido contrario. Siguiendo el convenio de signos en movimientos rectilíneos señalado anteriormente, esto significa que el movimiento ha cambiado su sentido y se dirige al punto de partida. Veamos:
Ahora, para determinar x04 podemos usar el valor de la recta en cualquier instante de tiempo, por ejemplo t = 50 s, quedando
Para el cuarto tramo, nos queda la ecuación del movimiento:
Tramo V ( 75 < t < 87.5 )
De nuevo, la pendiente ( velocidad ) en este tramo es igual en este caso a la del segundo tramo pero de sentido contrario. Siguiendo el convenio de signos en movimientos rectilíneos señalado anteriormente, esto significa que el movimiento ha cambiado su sentido y se dirige al punto de partida. Veamos:
Calculamos la posición inicial usando como referencia el punto final de la gráfica:
Finalmente, para el quinto tramo la ecuación del movimiento nos queda
Una vez obtenida la expresión para cada tramo, podemos dar una única expresión en forma de función definida a trozos:
Y para la velocidad...
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
