Área y perímetro a partir de triángulos rectángulos
Enunciado
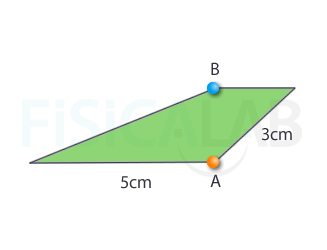
Determina el área y el perímetro de la siguiente figura.
Ten presente que la distancia entre los dos puntos señalados es de 2 cm.
Solución
Consideraciones previas
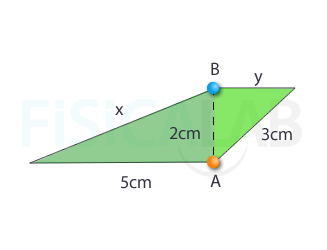
Si te fijas detenidamente, nos están dando una figura que está en realidad formada por dos triángulos rectángulos. Observa.
Recuerda que el perímetro de una figura geométrica es la suma de todos sus lados. En ese sentido nos restaría por calcular el valor de x e y. Por otro lado, para el cálculo del área sumaríamos las áreas de los dos triángulos rectángulos. Recuerda que el área de un triángulo es base por altura dividido entre dos.
Resolución
En primer lugar, calculamos x, que es la hipotenusa del primer triángulo. Para ello utilizamos el teorema de Pitágoras.
En relación a y, se trata del cateto del segundo triángulo rectángulo. Volvemos a aplicar Pitágoras, teniendo presente que la hipotenusa es el lado de 3cm y el cateto conocido el de 2cm:
Así pues, el perímetro buscado es P=5+3+5.38+2.23=15.61cm .
En relación al área, la de un triángulo se puede calcular como la mitad del producto de su base por su altura. Tenemos pues:
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.